yProcessingClub

すみません、許してください

AM変調信号のウィグナービレ分布

信号処理

今回も引き続き情報の精度については自信が無い．
メモとしてブログに残しておく．

yuri-processing-club.hatenablog.com

この記事で， $z(t)=A(t)\mathrm{e}^{j \phi (t)}$ のウィグナービレ分布は

$W_z(t,f) = \mathcal{W}_A(t, f-f_i(t))$
になることを計算で確かめた．

本記事ではこれの意味を考えていく．

f:id:Yuri-Processing-Club:20181114193536p:plain

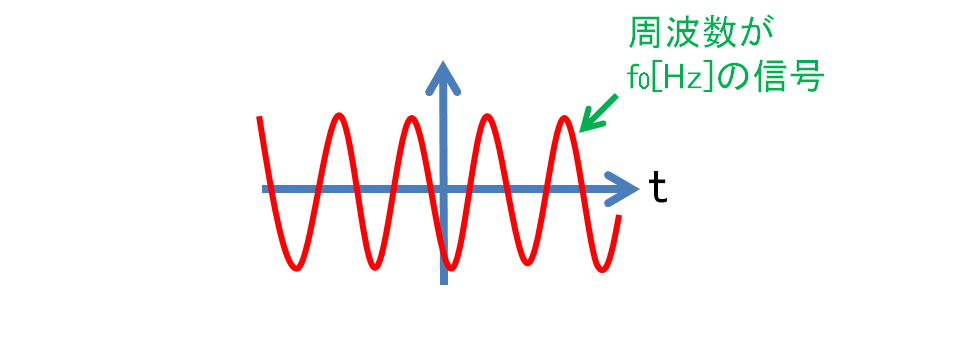
周波数一定（ $f_0$ ）の信号を $f_c$ で変調しよう．

f:id:Yuri-Processing-Club:20181114193459p:plain
スペクトルで見ると，このように $f_c$ だけ平行移動する形となる．

この例では元の信号の周波数 $f_0$ も搬送波 $f_c$ も時間変化しない．

f:id:Yuri-Processing-Club:20181114193558p:plain
時間周波数平面で書き直してみるとこんな感じ．周波数の時間変化は無いのでグラフの傾きは $0$ である．

次に $A(t)$ の周波数が時間変化する信号を考える．
搬送波周波数は一定なので，
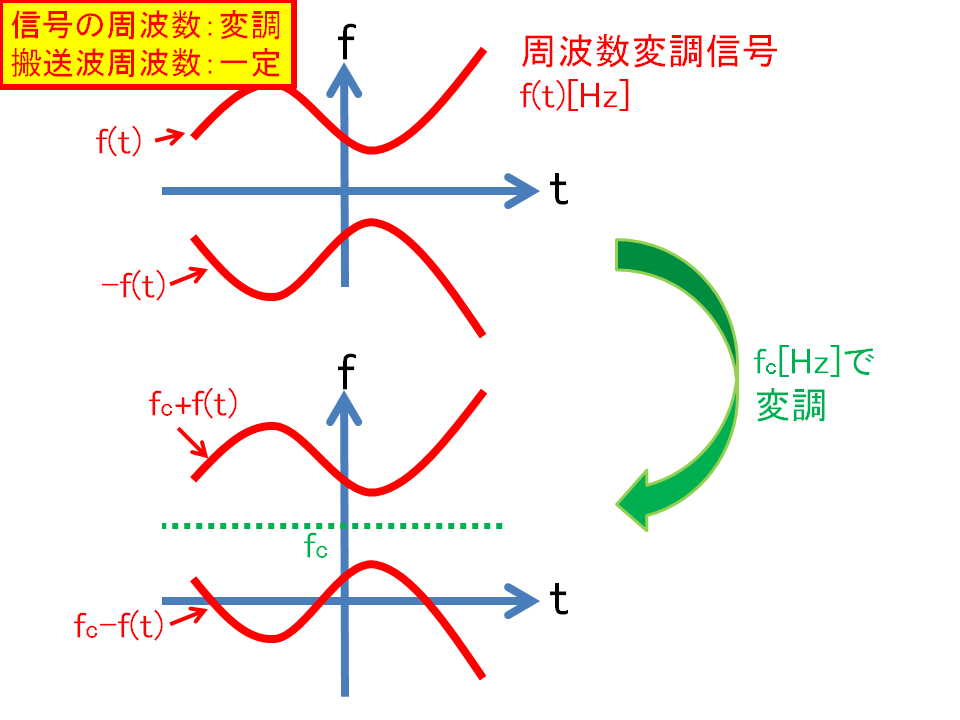
f:id:Yuri-Processing-Club:20181114193824p:plain

f:id:Yuri-Processing-Club:20181114193824p:plain

同じように $f_c$ だけ平行移動した形となる．

次に $A(t)$ も $f_c$ も変調する場合を考える．
f:id:Yuri-Processing-Club:20181114194006p:plain
ある時点 $t_1$ におけるもとの信号の周波数 $\pm f(t_1)$ はその時点での搬送波の周波数 $f_c(t_1)$ だけずれるので，変調後の周波数 $f'=f_c(t_1) \pm f(t_1)$

f:id:Yuri-Processing-Club:20181114200201p:plain

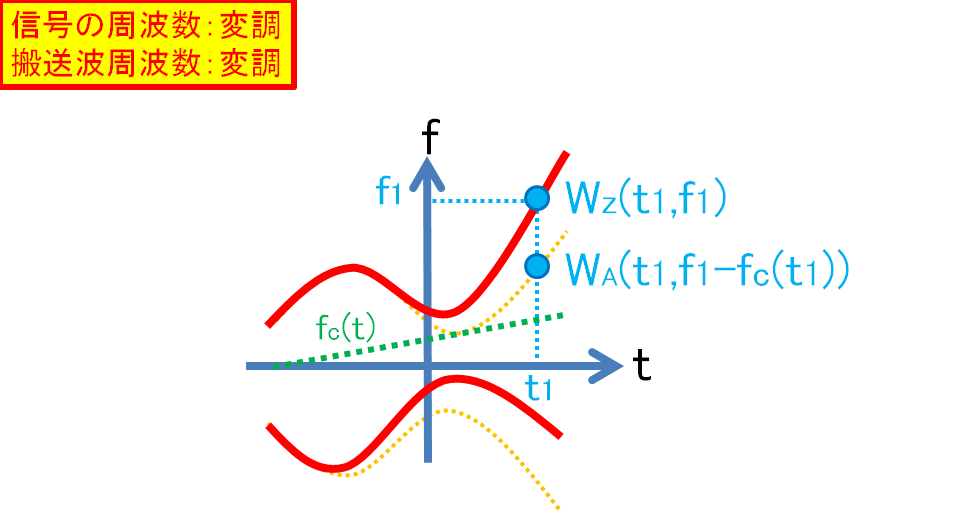
時間-周波数平面 $W(t,f)$ で考えると，変調後のある点 $W_z(t_1,f_1)$ は，変調前は $f_c(t_1)$ だけ下にあった．つまり変調前は $\mathcal{W}_A(t_1,f_1-f_c(t_1))$ の位置にあった．

変調する搬送波周波数 $f_c(t)$ を瞬時周波数 $f_i(t)$ に書き直して， $W_z(t,f) = \mathcal{W}_A(t, f-f_i(t))$ である．

振幅 $A(t)$ を瞬時周波数 $f_i(t)$ を使ってAM変調した信号のウィグナービレ分布 $W_z$ は， $f_i(t)$ と $A(t)$ のウィグナー分布 $\mathcal{W}_A$ を使って表せることが分かる．
若干煙に巻いた部分はあるが，何となくの解釈はこんな感じでよいかもしれないし，よくないかもしれない．