yProcessingClub

すみません、許してください

メモ：連続と離散の変換　積分

信号処理

数式の離散表現

　数学や信号処理をプログラミングで実装する際，注意すべきは連続と離散の取り違えである．数学などの専門書においては数式は連続型であるが，プログラミングする場合は離散型に適度に読み変える必要がある．今回は簡単に積分の離散表現を示す．

結論

y=s(t)の積分は以下．

Y=\int s(t)dt


これを離散的に表現すると，

y=s(nT_s)の積分は以下．

Y=\Sigma _{n=0} ^{N-1} T_s s(nT_s)

ここでT_sはサンプリング周期．

くわしい説明

y=s(t)はこういう形だとする．
f:id:Yuri-Processing-Club:20181108182004p:plain

これを時間間隔T_sでサンプリングしたのがs(nT_s)である．
f:id:Yuri-Processing-Club:20181108182223p:plain


Y=\int s(t)dtはグラフの面積を表している．

f:id:Yuri-Processing-Club:20181108182445p:plain

これを離散的に表現すると，T_s s(nT_s)で表される長方形の面積の合計値で近似することになる．

f:id:Yuri-Processing-Club:20181108182617p:plain

終わり

仕事でここを取り違えて大ポカをやらかしてしまったので，忘れないようにブログにてメモした．

瞬時周波数についてのふわっとした解釈

信号処理

記憶の整理のためにメモ．
記事の正しさに責任は持ちません．

追記。
↓qiitaに記事を投稿した。ブログ記事の焼き直しだが、より詳しく書いてるので良かったら見て欲しい。
qiita.com


瞬時周波数とは？

ある信号（音響信号など）の周波数の時間変化（変調と言ったりする）を調べたい欲求がある人もいるだろうが，そういうのを調べるのを時間周波数解析という．時間周波数解析において一番知りたいのは「（目的の信号の）周波数の時間変化」であり，これは位相を時間微分することで求められ，これを瞬時周波数と呼ぶことにする．（速度の時間変化は速度を微分すると求められ，これはどうやら加速度と言うらしいのだが，位相を微分したものは瞬時周波数と言う．）


簡単にまとめると，

ある一瞬の周波数を知りたい
　↓
位相を時間微分する

という素朴な考え方だ．


　　

周波数が一定の信号

周波数が時間変化する信号を考える前に，
まず周波数が一定の信号を考える．

振幅1，周波数f_0（一定）である信号s(t)
s(t)=\cos(2 \pi f_0 t)
ここで位相 2 \pi f_0 tを微分すると2 \pi f_0であり，瞬時周波数は時間変化せず、周波数が一定であることを再確認できる．

周波数が時間変化する信号

次に周波数が時間変化する信号を考える．
瞬時周波数をf'(t)で表す．

t=0[\mathrm s]でf'(0)=1000[\mathrm {Hz}]，
t=10[\mathrm s]でf'(10)=5000[\mathrm {Hz}]，
と周波数が線形変化する場合，
瞬時周波数の時間-周波数グラフは以下のようになる．

このグラフの式は
\begin{eqnarray*} f'(t)&=&\frac{5000-1000}{10-0}t + 1000\\ &=&400t+1000 \end{eqnarray*}

周波数の時間変化を見るには位相を微分すれば良かったので，逆向きに考えると，このような周波数の時間変化を持つ位相はf'(t)を積分すれば求められる．

\begin{eqnarray*} f(t)&=&\int f'(t)dt\\ &=&\int (400t+1000)dt\\ &=&200t^2+1000t \end{eqnarray*}

これを\cos()の中に入れると，
周波数が時間変化する信号
s(t)=\cos(2\pi(200t^2+1000t))
が出来上がる．
このスペクトログラムを求めると，

となり，期待通りの信号となった．

ちなみに，このように線形に周波数が変調する信号をLFM信号(Linear Frequency Modulated Signal，線形周波数変調信号)とか線形チャープ信号と言ったりする．

別の例

瞬時周波数が
g'(t) = 500\sin(2 \pi t) + 500t + 3000
となる信号を考える．
g'(t)のグラフは以下．

これもg'(t)を積分して，
g(t) = \int g'(t)dt = -\frac{500}{2 \pi} \cos(2 \pi t) + 250t^2 + 3000t
であり，これを\cos()に入れて，
信号s(t)=\cos\left( 2 \pi \left( -\frac{500}{2 \pi} \cos(2 \pi t) + 250t^2 + 3000t \right) \right)が出来上がる．
このスペクトログラムは

となって期待通りである．



TIME-FREQUENCY ANALYSIS Example 1.3

信号処理

TIME-FREQUENCY ANALYSISの例題を解き進める．

Example 1.3

\begin{eqnarray*} s(t) = (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t} \end{eqnarray*}
のBandwidth \sigma_\omegaを求めよ．



解答

解答方針

{\sigma_{\omega}}^2 = \langle \omega^2 \rangle - \langle \omega \rangle^2であり，

今回は1.4 SIMPLE CALCULATION TRICKSで紹介されている
\langle \omega \rangle = \int \omega |S(\omega)|^2d\omega=\int s^* (t) \frac{1}{j}\frac{d}{dt}s(t)dt
\begin{eqnarray*} \langle \omega^2 \rangle = \int \omega^2 |S(\omega)|^2d\omega&=&\int s^* (t) \left( \frac{1}{j}\frac{d}{dt} \right) ^2 s(t)dt\\ &=&-\int s^*(t)\frac{d^2}{dt^2}s(t)dt\\ &=&\int \left|\frac{d}{dt}s(t) \right|^2dt \end{eqnarray*}
の結果を用いて計算する．

\langle \omega \rangleの導出

\begin{eqnarray*} \frac{1}{j}\frac{d}{dt}s(t)&=&\frac{1}{j} (\alpha / \pi)^{1/4} \left( -\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t \right)' \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t}\\ &=& \frac{1}{j} (\alpha / \pi)^{1/4} \left( -\alpha t + j \beta t + j\omega_0 \right) \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t}\\ &=& (\alpha / \pi)^{1/4} \left( j\alpha t + \beta t + \omega_0 \right) \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t}\\ \end{eqnarray*}

s^*(t) = (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha t^2 /2 - j\beta t^2 /2 - j \omega_0 t}

\begin{eqnarray*} \langle \omega \rangle &=&\int s^* (t) \frac{1}{j}\frac{d}{dt}s(t)dt\\ &=& \int (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha t^2 /2 - j\beta t^2 /2 - j \omega_0 t} (\alpha / \pi)^{1/4} \left( j\alpha t + \beta t + \omega_0 \right) \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t}dt\\ &=& \sqrt{\frac{\alpha}{\pi}} \int \left( j\alpha t + \beta t + \omega_0 \right) \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{\pi}} \int \left( j\alpha t + \beta t \right) \mathrm{e}^{-\alpha t^2}dt + \omega_0\sqrt{\frac{\alpha}{\pi}} \int \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{\pi}} 0 + \omega_0 \sqrt{\frac{\alpha}{\pi}} \sqrt{\frac{\pi}{\alpha}}\\ &=& \omega_0 \end{eqnarray*}



\langle \omega^2 \rangleの導出

\begin{eqnarray*} \langle \omega^2 \rangle &=&\int \left|\frac{d}{dt}s(t) \right|^2dt\\ &=& \int \left| (\alpha / \pi)^{1/4} \left( -\alpha t + j \beta t + j\omega_0 \right) \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t} \right|^2 dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \int \left| -\alpha t + j \beta t + j\omega_0 \right|^2 \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \int \left( \left( \alpha t \right)^2 + \left( \beta t + \omega_0 \right)^2 \right) \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \int \left( \alpha^2 t ^2 + \beta ^2 t^2 + 2 \beta \omega_0 t + \omega_0 ^2 \right) \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \int \left( \left( \alpha^2 + \beta^2\right) t ^2 + 2 \beta \omega_0 t + \omega_0 ^2 \right) \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \left( \left( \alpha^2 + \beta^2 \right) \int t^2 \mathrm{e}^{-\alpha t^2}dt + 2 \beta \omega_0 \int t \mathrm{e}^{-\alpha t^2}dt+ \omega_0 ^2 \int \mathrm{e}^{-\alpha t^2}dt \right) \cdots (*)\\ &=& \sqrt{\frac{\alpha}{ \pi}} \left( \left( \alpha^2 + \beta^2 \right) \frac{1}{2 \alpha} \sqrt{\frac{\pi}{\alpha}} + 2 \beta \omega_0 0+ \omega_0 ^2 \sqrt{\frac{\pi}{\alpha}} \right) \cdots (**)\\ &=& \frac{\alpha^2 + \beta^2}{2 \alpha} + \omega_0 ^2 \end{eqnarray*}

(*)→(**)の変形に関しては，
ガウス積分の公式から\int t^2 \mathrm{e}^{-\alpha t^2}dt = \frac{1}{2 \alpha} \sqrt{\frac{\pi}{\alpha}}，\int \mathrm{e}^{-\alpha t^2}dt= \sqrt{\frac{\pi}{\alpha}}を用いた．
また， \int t^2 \mathrm{e}^{-\alpha t^2}dtは\int (偶関数) dt = 0である．

まとめ

\begin{eqnarray*} {\sigma_{\omega}}^2 &=& \langle \omega^2 \rangle - \langle \omega \rangle^2\\ &=& \frac{\alpha^2 + \beta^2}{2 \alpha} + \omega_0 ^2 - \omega_0 ^2\\ &=& \frac{\alpha^2 + \beta^2}{2 \alpha} \end{eqnarray*}

TIME-FREQUENCY ANALYSIS Example 1.1

信号処理

TIME-FREQUENCY ANALYSISの例題を解き進める．

Example 1.1

\begin{eqnarray*} s(t) = (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha(t-t_0)^2/2+j\varphi(t)} \end{eqnarray*}
の標準偏差\sigma_tを求めよ．



解答

{\sigma_t}^2 = \langle t^2 \rangle - \langle t \rangle^2より，
\langle t^2 \rangleと\langle t \rangleをそれぞれ求める．

\langle t \rangleの導出

\langle t \rangleは以下で与えられる．
\begin{eqnarray*} \langle t \rangle &=& \int t | s(t) |^2dt \end{eqnarray*}

まず | s(t) | を求める．
\begin{eqnarray*} | s(t) | &=& | (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha(t-t_0)^2/2+j\varphi(t)} |\\ &=& | (\alpha / \pi)^{1/4}| |\mathrm{e}^{-\alpha(t-t_0)^2/2} || \mathrm{e}^{j\varphi(t)} |\\ &=& (\alpha / \pi)^{1/4}\mathrm{e}^{-\alpha(t-t_0)^2/2} \end{eqnarray*}
（※ | \mathrm{e}^{j\varphi(t)} | = \sqrt{\mathrm{e}^{j\varphi(t)}\mathrm{e}^{-j\varphi(t)}}=1）

\begin{eqnarray*} \langle t \rangle &=& \int t | s(t) |^2dt\\ &=& \int t ( (\alpha / \pi)^{1/4}\mathrm{e}^{-\alpha(t-t_0)^2/2} )^2dt\\ &=& \int t ( (\alpha / \pi)^{1/2}\mathrm{e}^{-\alpha(t-t_0)^2} )dt\\ &=& \sqrt{\frac{\alpha}{\pi}}\int t \mathrm{e}^{-\alpha(t-t_0)^2} dt \end{eqnarray*}

次に\int t \mathrm{e}^{-\alpha(t-t_0)^2} dtを解く．
次のように変形する．
\int t \mathrm{e}^{-\alpha(t-t_0)^2} dt=\int (t-t_0) \mathrm{e}^{-\alpha(t-t_0)^2} dt + t_0 \int \mathrm{e}^{-\alpha(t-t_0)^2} dt
右辺第一項を解く．
t-t_0=vと置くと，
\int (t-t_0) \mathrm{e}^{-\alpha(t-t_0)^2} dt = \int v \mathrm{e}^{-\alpha v^2} dv
vは奇関数，\mathrm{e}^{-\alpha v^2}は偶関数なので，v \mathrm{e}^{-\alpha v^2}は奇関数．
よって， \int v \mathrm{e}^{-\alpha v^2} dv = 0となる．
次に右辺第二項を解くのだが，
ガウス積分の公式から\int \mathrm{e}^{-\alpha(t-t_0)^2} dt = \sqrt{\frac{\pi}{\alpha}}なので，
t_0 \int \mathrm{e}^{-\alpha(t-t_0)^2} dt = t_0 \sqrt{\frac{\pi}{\alpha}}
以上より，
\int t \mathrm{e}^{-\alpha(t-t_0)^2} dt = t_0 \sqrt{\frac{\pi}{\alpha}}

以上より，
\begin{eqnarray*} \langle t \rangle &=& \sqrt{\frac{\alpha}{\pi}}\int t \mathrm{e}^{-\alpha(t-t_0)^2} dt\\ &=& \sqrt{\frac{\alpha}{\pi}} t_0 \sqrt{\frac{\pi}{\alpha}}\\ &=& t_0 \end{eqnarray*}

\langle t^2 \rangleの導出

\langle t^2 \rangleは以下で与えられる．
\begin{eqnarray*} \langle t^2 \rangle &=& \int t^2 | s(t) |^2dt \end{eqnarray*}
\langle t \rangleを導出した際の結果を用いて，
\begin{eqnarray*} \langle t^2 \rangle &=& \int t^2 | s(t) |^2dt &=& \sqrt{\frac{\alpha}{\pi}}\int t^2 \mathrm{e}^{-\alpha(t-t_0)^2} dt \end{eqnarray*}

\int t^2 \mathrm{e}^{-\alpha(t-t_0)^2} dtのところを解く．
\begin{eqnarray*} \int t^2 \mathrm{e}^{-\alpha(t-t_0)^2} dt &=& \int (t-t_0)^2 \mathrm{e}^{-\alpha(t-t_0)^2}dt + 2t_0 \int t \mathrm{e}^{-\alpha(t-t_0)^2}dt - {t_0}^2 \int \mathrm{e}^{-\alpha(t-t_0)^2}dt\\ &=& \frac{1}{2\alpha} \sqrt{\frac{\pi}{\alpha}} +2t_0 \times t_0 \sqrt{\frac{\pi}{\alpha}} - {t_0} ^2 \times \sqrt{\frac{\pi}{\alpha}}\\ &=&\frac{1}{2\alpha} \sqrt{\frac{\pi}{\alpha}} + {t_0} ^2 \sqrt{\frac{\pi}{\alpha}} \end{eqnarray*}
（ガウス積分より　\int (t-t_0)^2 \mathrm{e}^{-\alpha(t-t_0)^2}dt = \int v^2 \mathrm{e}^{-\alpha v^2}dv = \frac{1}{2\alpha} \sqrt{\frac{\pi}{\alpha}}を用いた）


よって，
\begin{eqnarray*} \langle t^2 \rangle &=& \sqrt{\frac{\alpha}{\pi}}\int t^2 \mathrm{e}^{-\alpha(t-t_0)^2} dt\\ &=& \sqrt{\frac{\alpha}{\pi}} \left( \frac{1}{2\alpha} \sqrt{\frac{\pi}{\alpha}} + {t_0} ^2 \sqrt{\frac{\pi}{\alpha}} \right)\\ &=& \frac{1}{2\alpha} +{t_0} ^2 \end{eqnarray*}


以上より，
\begin{eqnarray*} {\sigma_t}^2 &=& \langle t^2 \rangle - \langle t \rangle^2\\ &=&\frac{1}{2\alpha} +{t_0} ^2 - {t_0} ^2\\ &=& \frac{1}{2\alpha} \end{eqnarray*}

メモ：コーエンクラス　核関数を使うとクロス項が消えるりくつ

信号処理

メモ．
検証していないので，情報に対して責任は一切持ちません．

コーエンクラスはウィグナー分布に似た形の関数＝曖昧度関数と核関数の畳み込みとなっている．
核関数は何をしてるかっていうと，どうやらクロス項を抑制しているっぽい．
なんでクロス項を抑制できるの？と疑問である．
その辺は現在勉強中であるが，どうやら以下のようなイメージらしい．

f:id:Yuri-Processing-Club:20181101174248p:plain
f:id:Yuri-Processing-Club:20181101174257p:plain
核関数はチョイウィリアムス．
値は暗赤色=1，暗青色=0で，原点回りの値を抽出するようなフィルタである．

検証については，
実験的には曖昧度関数などを描いて信号が原点を通る直線になるのか確かめる．
理論的には曖昧度関数の勉強
が必要である．

仕事忙しくなってきたので検証はかなり後になりそう．

【信号処理基礎】実信号の解析信号への変換方法

信号処理

自分用メモ．計算が合ってるかは自信が無い．
何かあればコメントいただけるとありがたいです．

時間周波数解析手法の一種であるウィグナー分布において，正負の周波数成分を持つ信号や二つ以上の成分から成る信号を分析してみると，その中間部分にスペクトルが発生し，これをクロス項という．本来信号が無いはずの部分にスペクトルが出ているのはよろしくない（そのためクロス項を抑制するような研究が多くなされている）．クロス項抑制のためには実信号を負の周波数を含まないような複素信号に変換してからウィグナー分布の計算を行う．負の周波数を含まない複素信号を解析信号という．今回は実信号から解析信号に変換する計算方法を詳しく書く．

解析信号をz(t)，実信号をg(t)，g(t)のフーリエ変換をG(\omega)とする．

\begin{eqnarray*} z(t) &=& \frac{1}{2\pi} \int_{-\infty}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega\\ &=& 2 \frac{1}{2\pi} \int_{0}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega\\ &=& \frac{1}{\pi} \int_{0}^{\infty} \int_{-\infty}^{\infty} g(k) \mathrm{e}^{-j \omega k} dk \mathrm{e}^{j \omega t} d\omega\\ &=& \frac{1}{\pi} \int_{0}^{\infty} \int_{-\infty}^{\infty} g(k) \mathrm{e}^{j \omega (t-k)} dkd\omega\\ &=& \frac{1}{\pi} \int_{-\infty}^{\infty} g(k) \left( \pi \delta(t-k) + \frac{j}{t-k} \right) dk\\ &=& \int_{-\infty}^{\infty} g(k) \delta(t-k) dk + \frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk \\ &=& g(t) + \frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk \\ &=& g(t)+j\mathcal{H}(g(t)) \end{eqnarray*}


更に詳しい説明．

これは普通の逆フーリエ変換である．
z(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega

次に負の周波数を消し去る．ここの計算が本質部分である．
\frac{1}{2\pi} \int_{-\infty}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega = 2 \frac{1}{2\pi} \int_{0}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega= \frac{1}{\pi} \int_{0}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega

次にG(\omega)=\int_{-\infty}^{\infty} g(k) \mathrm{e}^{-j \omega k} dkとして入れる．
\frac{1}{\pi} \int_{0}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega = \frac{1}{\pi} \int_{0}^{\infty} \int_{-\infty}^{\infty} g(k) \mathrm{e}^{-j \omega k} dk \mathrm{e}^{j \omega t} d\omega

\mathrm{e}^{-j \omega k}と\mathrm{e}^{j \omega t}をくっつけて，積分順序を入れ替える．
\frac{1}{\pi} \int_{0}^{\infty} \int_{-\infty}^{\infty} g(k) \mathrm{e}^{j \omega (t-k)} dkd\omega = \frac{1}{\pi} \int_{-\infty}^{\infty} g(k) \int_{0}^{\infty} \mathrm{e}^{j \omega(t-k)} d\omega dk

内側の\int_{0}^{\infty} \mathrm{e}^{j \omega(t-k)} d\omegaを計算するが，ここで
\begin{equation} \int_{0}^{\infty} \mathrm{e}^{j \omega x} d\omega= \pi \delta(x) + \frac{j}{x} \end{equation}
を用いる．（この計算はここでは詳しく計算しない．結果だけ用いる．）
\int_{0}^{\infty} \mathrm{e}^{j \omega(t-k) } d\omega= \pi \delta(t-k) + \frac{j}{t-k}

内側の積分結果を元の式に代入して，第一項と第二項を分離する．
\frac{1}{\pi} \int_{-\infty}^{\infty} g(k) \left( \pi \delta(t-k) + \frac{j}{t-k} \right) dk= \int_{-\infty}^{\infty} g(k) \left(\delta(t-k) \right) dk + \frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk

第一項の\int_{-\infty}^{\infty} g(k) \delta(t-k) dkはkについての積分だが，k=tの時のみ\delta=1なので，
\int_{-\infty}^{\infty} g(k) \delta(t-k) dk=g(t)

第二項の\frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dkだが，\frac{1}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dkの部分はヒルベルト変換なので，
\frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk = j\mathcal{H}(g(t))と書く．

以上をまとめて，
z(t) =g(t)+j\mathcal{H}(g(t))

となる．



参考

matlab 信号の両端を滑らかに0にする場合はコサインテーパーを使う

matlab 信号処理

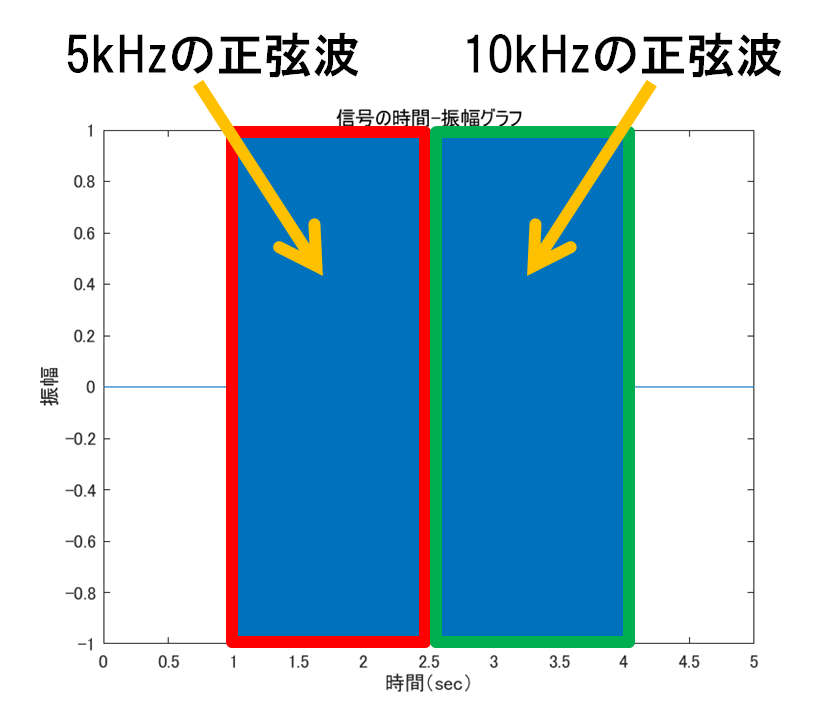
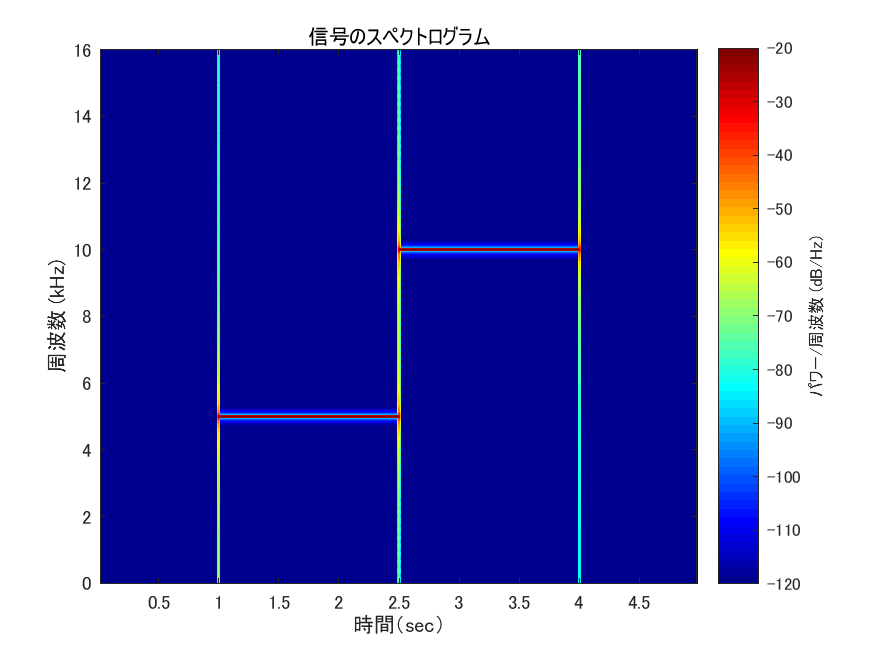
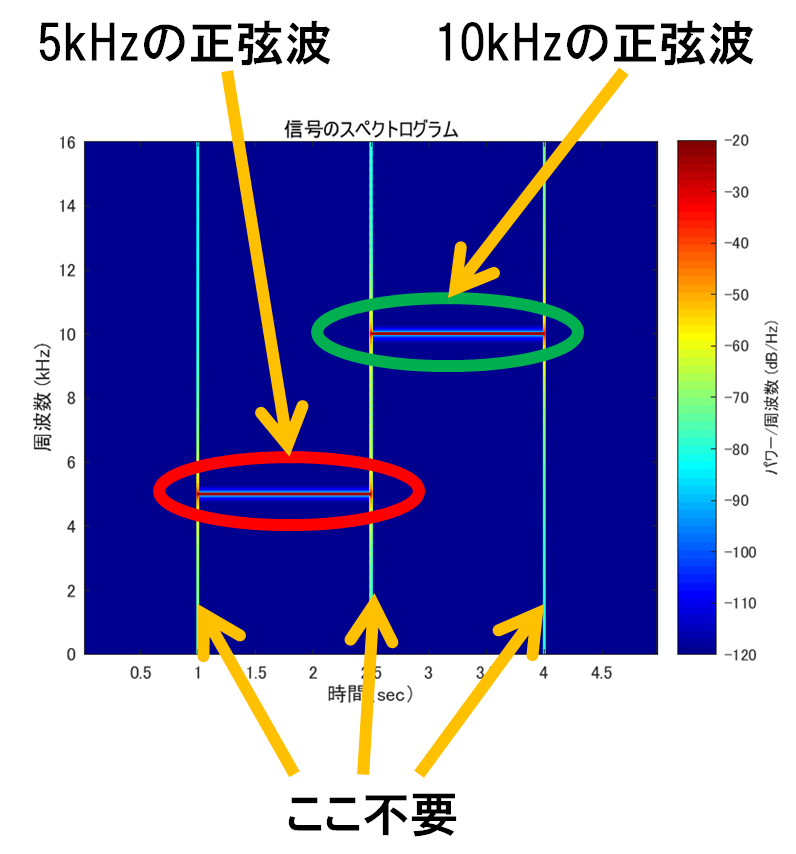
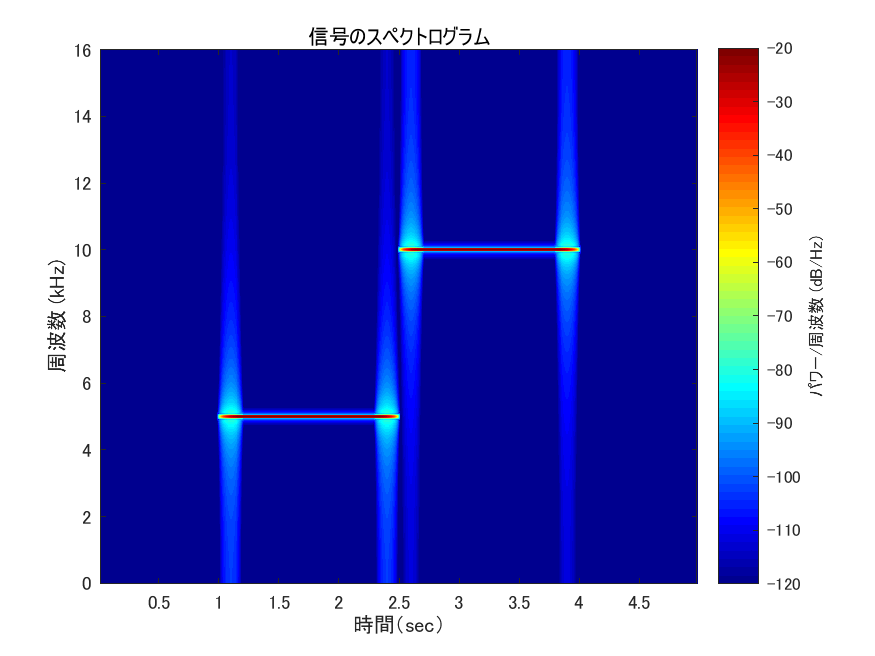
　実験用に正弦信号を作成することがある．例として1～1.5秒部分に5kHzの正弦波，1.5～3秒部分に10kHzの正弦波が含まれる信号の時間-振幅グラフを図1に，スペクトログラムを図2に示す（スペクトログラムを表示する部分までのmatlabコードを下に示す）．スペクトログラムを見ると信号の開始時点及び終了時点において，周波数の広い範囲に大きい値が出ている（図3）．これは信号が突然0→1に立ち上がる（終了時点では1→0になる）ことから，その時点においてあらゆる周波数が反応するのは当然である．しかしA[Hz]の正弦信号を入力したらA[Hz]のところにだけ値が出て来て欲しいわけで，そういうときは普通ならばスペクトログラムのウィンドウ幅を長くするなど分析側のパラメータを調整する必要がある．今回は理想的な信号が入ってくる場合の分析器の挙動を見たいので，分析側のパラメータを変えずに，実験用の信号を理想的なものに調整して綺麗な結果を出してみる．

f:id:Yuri-Processing-Club:20181003162409p:plain:w400
図 1: 信号の時間-振幅グラフ

f:id:Yuri-Processing-Club:20181003161738p:plain:w400
図 2: 信号のスペクトログラム

f:id:Yuri-Processing-Club:20181003163917p:plain:w400
図 3: 信号のスペクトログラム（説明付）



% 
% 信号を生成してスペクトログラムを表示する
% 
clear all;
close all;
clc

Fs = 32000;
SNRdB = -10;

% 信号を生成する
t1 = 1.5;
f1 = 5000;
N = Fs * t1;
t = ((1:N)-1)/Fs;
s1 = sin(2*pi*f1*t);
t2 = 1.5;
f2 = 10000;
N = Fs * t2;
t = ((1:N)-1)/Fs;
s2 = sin(2*pi*f2*t);
s0 = horzcat(s1, s2);
% 信号の前後にpad_time秒間の無音部分をくっつける
pad_time = 1;
s = padarray(s0, [0 round(pad_time * Fs)], 0, 'both');

% 時間グラフを描く
N = length(s);
t = ((1:N)-1)/Fs;
figure
plot(t, s);
title('信号の時間-振幅グラフ');
xlabel('時間（sec）');
ylabel('振幅');

% 信号のスペクトログラムを描画
Nw = 1024;
Nol = Nw*3/4;
NFFT = Nw;
figure;
spectrogram(s, Nw, Nol, NFFT, Fs, 'yaxis'); %ハミング窓
title('信号のスペクトログラム');
xlabel('時間（sec）');
colormap 'jet'
caxis_max = -20;
caxis_min = -120;
caxis([caxis_min, caxis_max]);


つまりこういうことをしたいわけである．

f:id:Yuri-Processing-Club:20181003165529p:plain:w500
図 4: 立ち上がり立ち下りが滑らかな信号の時間-振幅グラフ

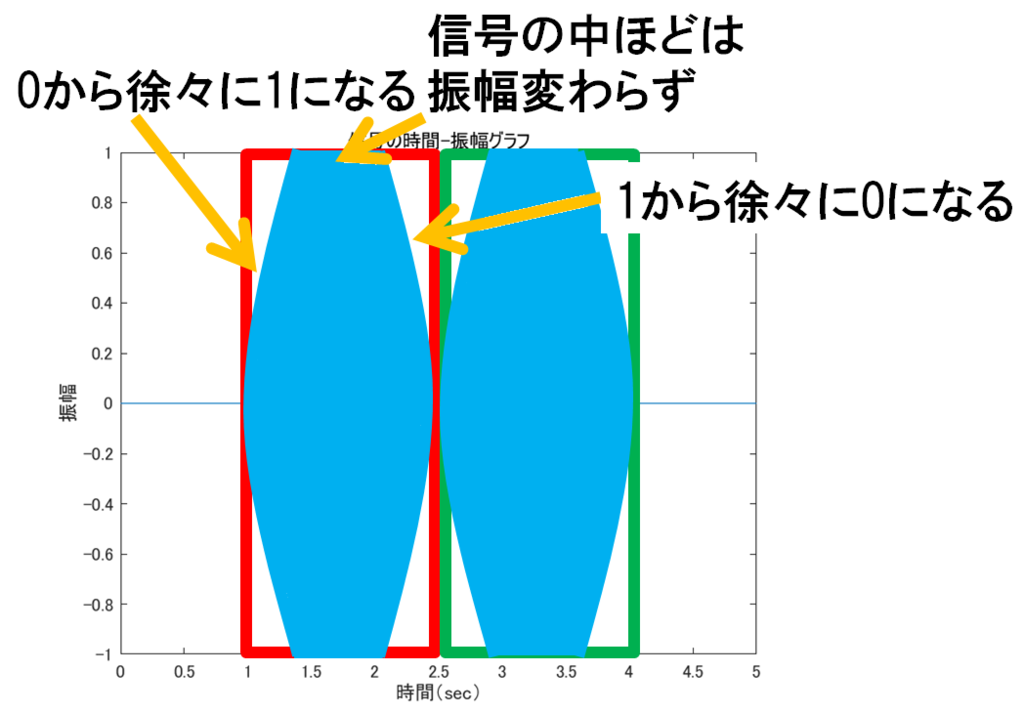
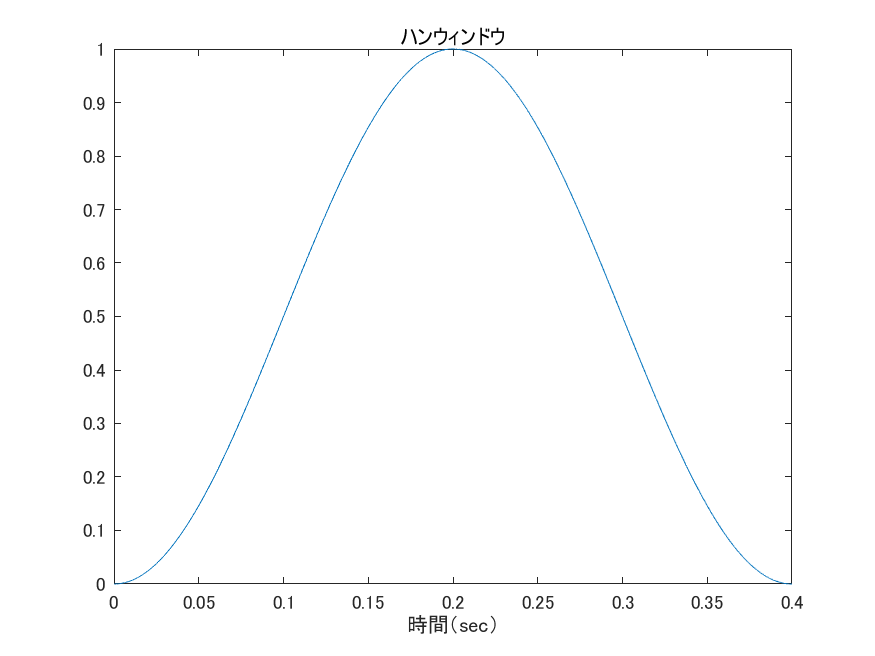
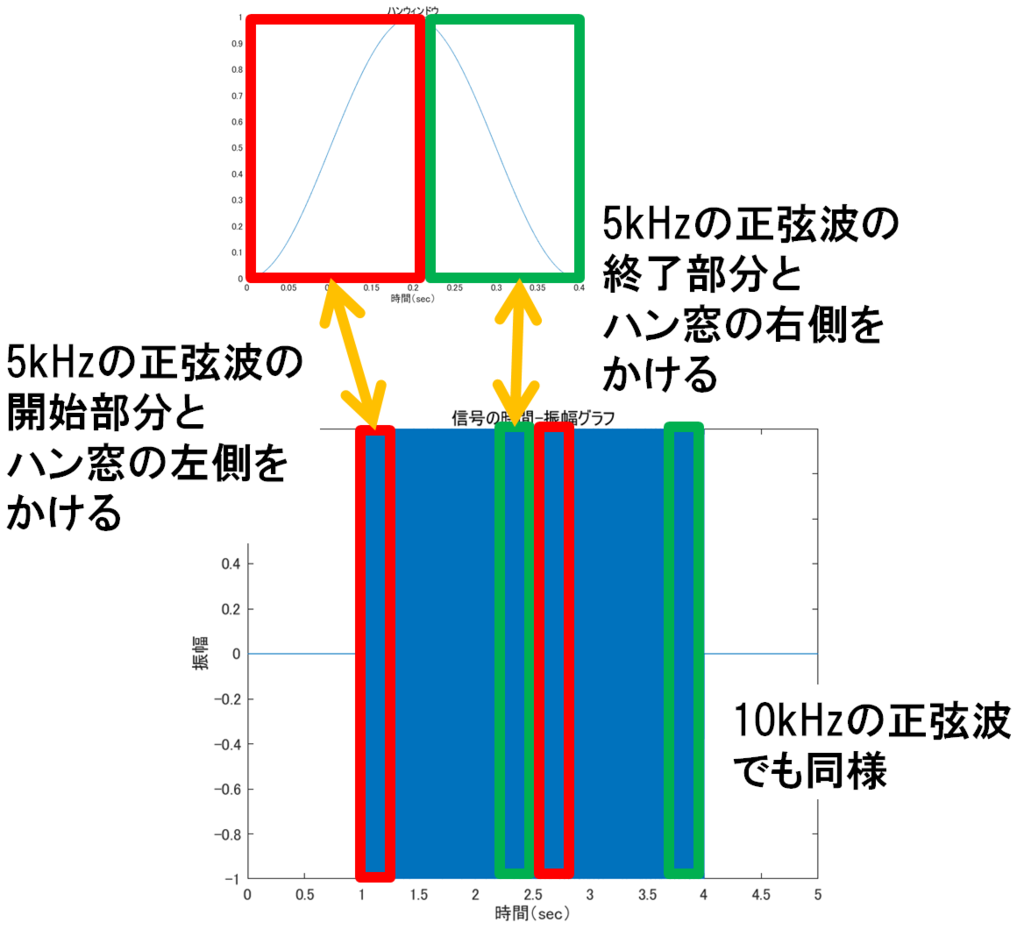
信号の最初と終わりの部分だけ窓関数を掛けたような形である．ネタバレするとコサインテーパーウィンドウを掛けてやればいいわけだが，最初はハンウィンドウを前半後半に分けて信号の最初と終わりにそれぞれ掛けるというやり方を取っていた．

f:id:Yuri-Processing-Club:20181003171032p:plain:w400
図 5: ハンウィンドウ

f:id:Yuri-Processing-Club:20181003171715p:plain
図 6: ハンウィンドウを分割して信号の前後とかけあわせるやつの説明

%
% 上のコードの「信号を生成する」 の部分を下に入れ替える
%
% 信号の両端に少しだけ窓関数をかける
single_sided_window_length_sec = 0.2;% 片側窓関数がかけられる時間
single_sided_window_length = single_sided_window_length_sec * Fs;% 窓関数の片側の長さ
w = hann(single_sided_window_length * 2);% ハン窓を作成
figure
N = length(w);
t = ((1:N)-1)/Fs;
plot(t, w);
title('ハンウィンドウ');
xlabel('時間（sec）');

% 信号を生成する
t1 = 1.5;
f1 = 5000;
N = Fs * t1;
t = ((1:N)-1)/Fs;
s1 = sin(2*pi*f1*t);
% 窓関数をかける
s1(1:single_sided_window_length) = w(1:single_sided_window_length)' .* s1(1:single_sided_window_length);% 左側
s1(end-single_sided_window_length+1:end) = w(single_sided_window_length+1:end)' .* s1(end-single_sided_window_length+1:end);% 右側

t2 = 1.5;
f2 = 10000;
N = Fs * t2;
t = ((1:N)-1)/Fs;
s2 = sin(2*pi*f2*t);
% 窓関数をかける
s2(1:single_sided_window_length) = w(1:single_sided_window_length)' .* s2(1:single_sided_window_length);% 左側
s2(end-single_sided_window_length+1:end) = w(single_sided_window_length+1:end)' .* s2(end-single_sided_window_length+1:end);% 右側

s0 = horzcat(s1, s2);

% 信号の前後にpad_time秒間の無音部分をくっつける
pad_time = 1;
s = padarray(s0, [0 round(pad_time * Fs)], 0, 'both');

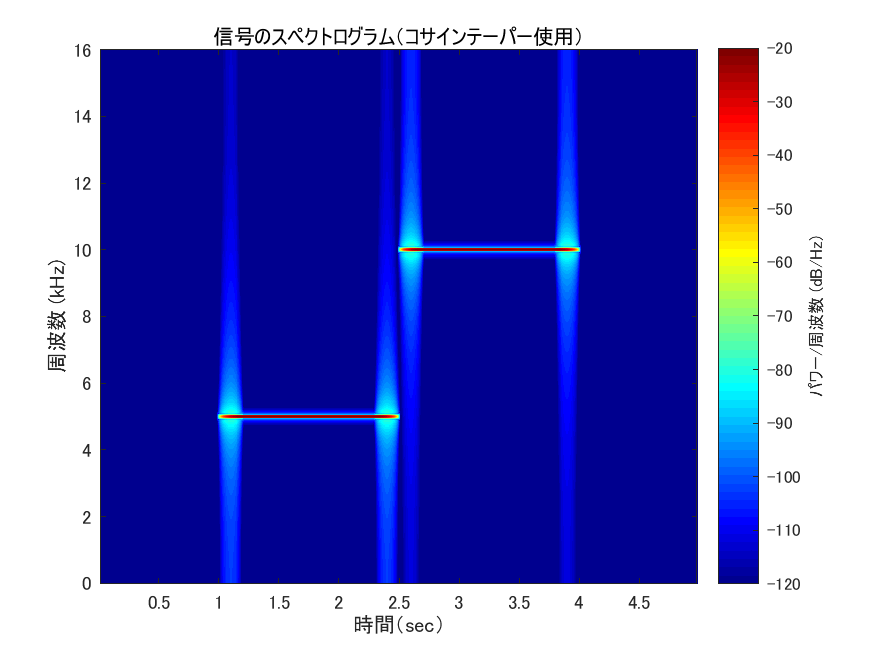
ハンウィンドウを分割して信号の前後にかけたものの時間-振幅グラフを図7，スペクトログラムを図8にそれぞれ示す．0→1に滑らかに変化しているので，スペクトログラムで欲しいところだけに信号が表示されている．

f:id:Yuri-Processing-Club:20181003174159p:plain:w400
図 7: 立ち上がり立ち下りを滑らかにした信号の時間-振幅グラフ

f:id:Yuri-Processing-Club:20181003174145p:plain:w400
図 8: 立ち上がり立ち下りを滑らかにした信号のスペクトログラム


こんなめんどくさいこと，やる？と思い上司に上手いやり方は無いか相談したところ，そういう場合は普通はコサインテーパーを使うとのこと．jp.mathworks.com
コサインテーパーウィンドウは開始部分及び終了部分がコサインの形をしていて，真ん中あたりは値が1のウィンドウである．信号と同じ長さのコサインテーパーウィンドウを用意して，信号にかけてやればOKである．
f:id:Yuri-Processing-Club:20181003180521p:plain:w400
図 9: 立ち上がり立ち下りを滑らかにした信号の時間-振幅グラフ（コサインテーパー使用）

%
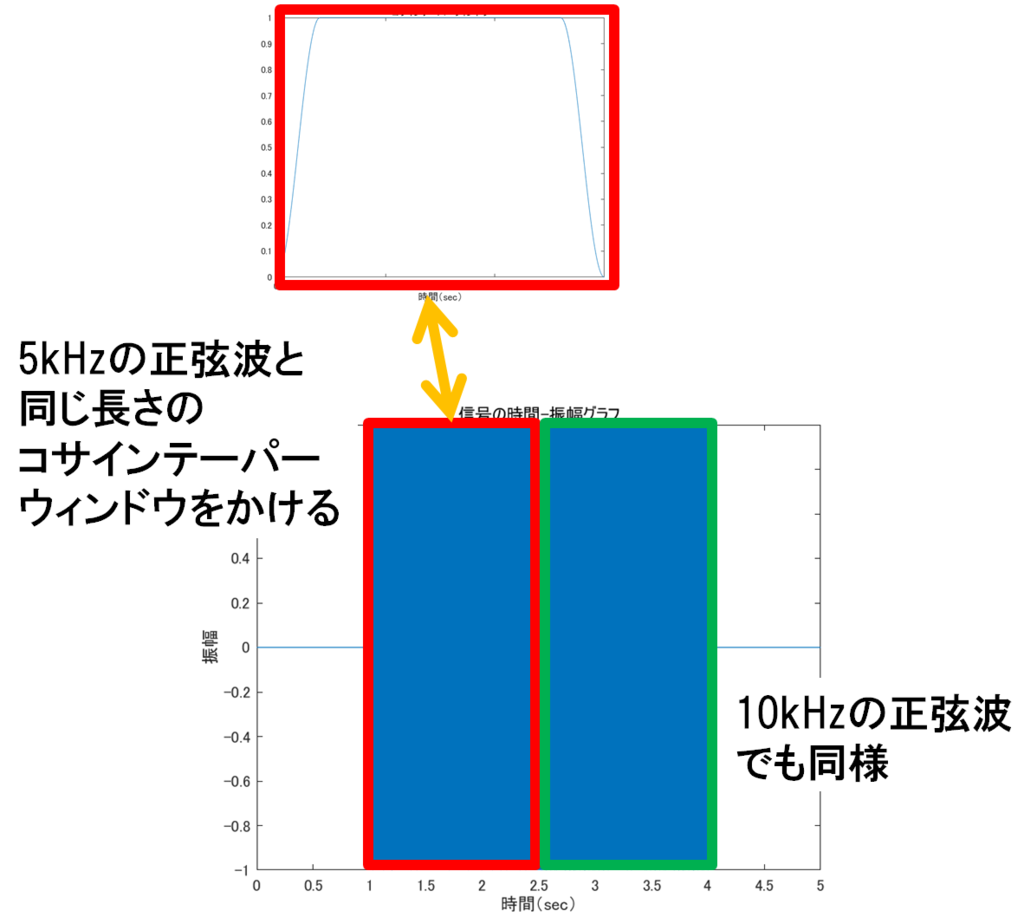
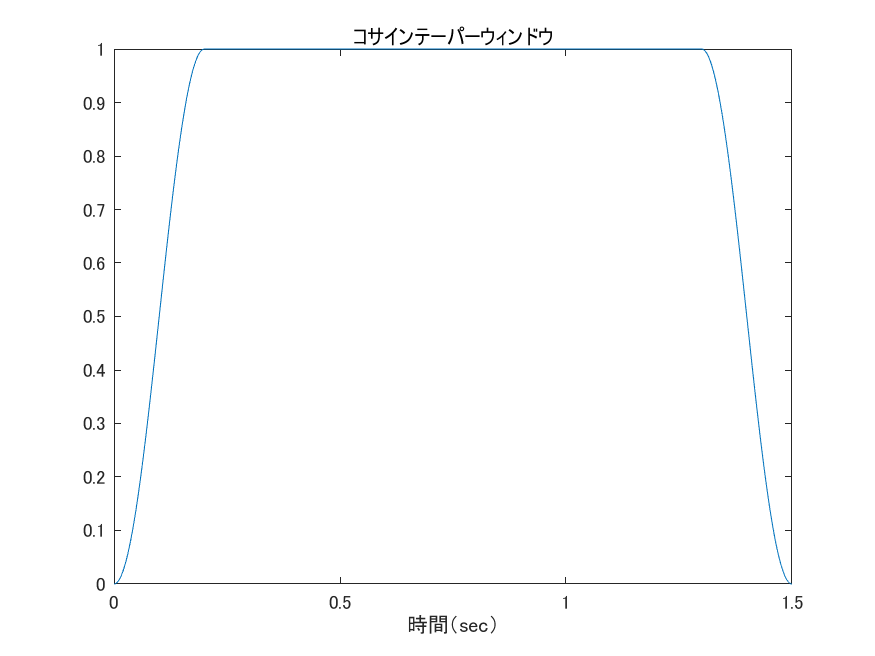
% 上のコードの「信号を生成する」 の部分を下に入れ替える
%
single_sided_window_length_sec = 0.2;% 片側窓関数がかけられる時間

% 信号を生成する
t1 = 1.5;
f1 = 5000;
N = Fs * t1;
t = ((1:N)-1)/Fs;
s1 = sin(2*pi*f1*t);
% 窓関数をかける
window_signal_length_ratio = (single_sided_window_length_sec*2)/t1;% 窓関数がかけられる時間の比
w = tukeywin(N, window_signal_length_ratio);
figure
plot(t, w);
title('コサインテーパーウィンドウ');
xlabel('時間（sec）');
s1 = w' .* s1;

t2 = 1.5;
f2 = 10000;
N = Fs * t2;
t = ((1:N)-1)/Fs;
s2 = sin(2*pi*f2*t);
% 窓関数をかける
window_signal_length_ratio = (single_sided_window_length_sec*2)/t2;% 窓関数がかけられる時間の比
w = tukeywin(N, window_signal_length_ratio);
% 5kHzのコサインテーパーウィンドウと同じなのでグラフは省略
s2 = w' .* s2;

s0 = horzcat(s1, s2);

% 信号の前後にpad_time秒間の無音部分をくっつける
pad_time = 1;
s = padarray(s0, [0 round(pad_time * Fs)], 0, 'both');

f:id:Yuri-Processing-Club:20181003180010p:plain:w400
図 10: コサインテーパーウィンドウ

f:id:Yuri-Processing-Club:20181003175920p:plain:w400
図 11: 立ち上がり立ち下りを滑らかにした信号の時間-振幅グラフ（コサインテーパー使用）

f:id:Yuri-Processing-Club:20181003180853p:plain:w400
図 12: 立ち上がり立ち下りを滑らかにした信号のスペクトログラム（コサインテーパー使用）