2018-11-07

TIME-FREQUENCY ANALYSIS Example 1.3

信号処理

Example 1.3

$\begin{eqnarray*} s(t) = (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t} \end{eqnarray*}$
のBandwidth $\sigma_\omega$ を求めよ．

解答

解答方針

${\sigma_{\omega}}^2 = \langle \omega^2 \rangle - \langle \omega \rangle^2$ であり，

今回は1.4 SIMPLE CALCULATION TRICKSで紹介されている
$\langle \omega \rangle = \int \omega |S(\omega)|^2d\omega=\int s^* (t) \frac{1}{j}\frac{d}{dt}s(t)dt$
$\begin{eqnarray*} \langle \omega^2 \rangle = \int \omega^2 |S(\omega)|^2d\omega&=&\int s^* (t) \left( \frac{1}{j}\frac{d}{dt} \right) ^2 s(t)dt\\ &=&-\int s^*(t)\frac{d^2}{dt^2}s(t)dt\\ &=&\int \left|\frac{d}{dt}s(t) \right|^2dt \end{eqnarray*}$
の結果を用いて計算する．

$\langle \omega \rangle$ の導出

$\begin{eqnarray*} \frac{1}{j}\frac{d}{dt}s(t)&=&\frac{1}{j} (\alpha / \pi)^{1/4} \left( -\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t \right)' \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t}\\ &=& \frac{1}{j} (\alpha / \pi)^{1/4} \left( -\alpha t + j \beta t + j\omega_0 \right) \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t}\\ &=& (\alpha / \pi)^{1/4} \left( j\alpha t + \beta t + \omega_0 \right) \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t}\\ \end{eqnarray*}$

$s^*(t) = (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha t^2 /2 - j\beta t^2 /2 - j \omega_0 t}$

$\begin{eqnarray*} \langle \omega \rangle &=&\int s^* (t) \frac{1}{j}\frac{d}{dt}s(t)dt\\ &=& \int (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha t^2 /2 - j\beta t^2 /2 - j \omega_0 t} (\alpha / \pi)^{1/4} \left( j\alpha t + \beta t + \omega_0 \right) \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t}dt\\ &=& \sqrt{\frac{\alpha}{\pi}} \int \left( j\alpha t + \beta t + \omega_0 \right) \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{\pi}} \int \left( j\alpha t + \beta t \right) \mathrm{e}^{-\alpha t^2}dt + \omega_0\sqrt{\frac{\alpha}{\pi}} \int \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{\pi}} 0 + \omega_0 \sqrt{\frac{\alpha}{\pi}} \sqrt{\frac{\pi}{\alpha}}\\ &=& \omega_0 \end{eqnarray*}$

$\langle \omega^2 \rangle$ の導出

$\begin{eqnarray*} \langle \omega^2 \rangle &=&\int \left|\frac{d}{dt}s(t) \right|^2dt\\ &=& \int \left| (\alpha / \pi)^{1/4} \left( -\alpha t + j \beta t + j\omega_0 \right) \mathrm{e}^{-\alpha t^2 /2 + j\beta t^2 /2 + j \omega_0 t} \right|^2 dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \int \left| -\alpha t + j \beta t + j\omega_0 \right|^2 \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \int \left( \left( \alpha t \right)^2 + \left( \beta t + \omega_0 \right)^2 \right) \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \int \left( \alpha^2 t ^2 + \beta ^2 t^2 + 2 \beta \omega_0 t + \omega_0 ^2 \right) \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \int \left( \left( \alpha^2 + \beta^2\right) t ^2 + 2 \beta \omega_0 t + \omega_0 ^2 \right) \mathrm{e}^{-\alpha t^2}dt\\ &=& \sqrt{\frac{\alpha}{ \pi}} \left( \left( \alpha^2 + \beta^2 \right) \int t^2 \mathrm{e}^{-\alpha t^2}dt + 2 \beta \omega_0 \int t \mathrm{e}^{-\alpha t^2}dt+ \omega_0 ^2 \int \mathrm{e}^{-\alpha t^2}dt \right) \cdots (*)\\ &=& \sqrt{\frac{\alpha}{ \pi}} \left( \left( \alpha^2 + \beta^2 \right) \frac{1}{2 \alpha} \sqrt{\frac{\pi}{\alpha}} + 2 \beta \omega_0 0+ \omega_0 ^2 \sqrt{\frac{\pi}{\alpha}} \right) \cdots (**)\\ &=& \frac{\alpha^2 + \beta^2}{2 \alpha} + \omega_0 ^2 \end{eqnarray*}$

$(*)$ → $(**)$ の変形に関しては，
ガウス積分の公式から $\int t^2 \mathrm{e}^{-\alpha t^2}dt = \frac{1}{2 \alpha} \sqrt{\frac{\pi}{\alpha}}$ ， $\int \mathrm{e}^{-\alpha t^2}dt= \sqrt{\frac{\pi}{\alpha}}$ を用いた．
また， $\int t^2 \mathrm{e}^{-\alpha t^2}dt$ は $\int (偶関数) dt = 0$ である．

まとめ

$\begin{eqnarray*} {\sigma_{\omega}}^2 &=& \langle \omega^2 \rangle - \langle \omega \rangle^2\\ &=& \frac{\alpha^2 + \beta^2}{2 \alpha} + \omega_0 ^2 - \omega_0 ^2\\ &=& \frac{\alpha^2 + \beta^2}{2 \alpha} \end{eqnarray*}$

2018-11-06

TIME-FREQUENCY ANALYSIS Example 1.1

信号処理

TIME-FREQUENCY ANALYSISの例題を解き進める．

Example 1.1

$\begin{eqnarray*} s(t) = (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha(t-t_0)^2/2+j\varphi(t)} \end{eqnarray*}$
の標準偏差 $\sigma_t$ を求めよ．

解答

${\sigma_t}^2 = \langle t^2 \rangle - \langle t \rangle^2$ より，
$\langle t^2 \rangle$ と $\langle t \rangle$ をそれぞれ求める．

$\langle t \rangle$ の導出

$\langle t \rangle$ は以下で与えられる．
$\begin{eqnarray*} \langle t \rangle &=& \int t | s(t) |^2dt \end{eqnarray*}$

まず $| s(t) |$ を求める．
$\begin{eqnarray*} | s(t) | &=& | (\alpha / \pi)^{1/4} \mathrm{e}^{-\alpha(t-t_0)^2/2+j\varphi(t)} |\\ &=& | (\alpha / \pi)^{1/4}| |\mathrm{e}^{-\alpha(t-t_0)^2/2} || \mathrm{e}^{j\varphi(t)} |\\ &=& (\alpha / \pi)^{1/4}\mathrm{e}^{-\alpha(t-t_0)^2/2} \end{eqnarray*}$
（※ $| \mathrm{e}^{j\varphi(t)} | = \sqrt{\mathrm{e}^{j\varphi(t)}\mathrm{e}^{-j\varphi(t)}}=1$ ）

$\begin{eqnarray*} \langle t \rangle &=& \int t | s(t) |^2dt\\ &=& \int t ( (\alpha / \pi)^{1/4}\mathrm{e}^{-\alpha(t-t_0)^2/2} )^2dt\\ &=& \int t ( (\alpha / \pi)^{1/2}\mathrm{e}^{-\alpha(t-t_0)^2} )dt\\ &=& \sqrt{\frac{\alpha}{\pi}}\int t \mathrm{e}^{-\alpha(t-t_0)^2} dt \end{eqnarray*}$

次に $\int t \mathrm{e}^{-\alpha(t-t_0)^2} dt$ を解く．
次のように変形する．
$\int t \mathrm{e}^{-\alpha(t-t_0)^2} dt=\int (t-t_0) \mathrm{e}^{-\alpha(t-t_0)^2} dt + t_0 \int \mathrm{e}^{-\alpha(t-t_0)^2} dt$
右辺第一項を解く．
$t-t_0=v$ と置くと，
$\int (t-t_0) \mathrm{e}^{-\alpha(t-t_0)^2} dt = \int v \mathrm{e}^{-\alpha v^2} dv$
$v$ は奇関数， $\mathrm{e}^{-\alpha v^2}$ は偶関数なので， $v \mathrm{e}^{-\alpha v^2}$ は奇関数．
よって， $\int v \mathrm{e}^{-\alpha v^2} dv = 0$ となる．
次に右辺第二項を解くのだが，
ガウス積分の公式から $\int \mathrm{e}^{-\alpha(t-t_0)^2} dt = \sqrt{\frac{\pi}{\alpha}}$ なので，
$t_0 \int \mathrm{e}^{-\alpha(t-t_0)^2} dt = t_0 \sqrt{\frac{\pi}{\alpha}}$
以上より，
$\int t \mathrm{e}^{-\alpha(t-t_0)^2} dt = t_0 \sqrt{\frac{\pi}{\alpha}}$

以上より，
$\begin{eqnarray*} \langle t \rangle &=& \sqrt{\frac{\alpha}{\pi}}\int t \mathrm{e}^{-\alpha(t-t_0)^2} dt\\ &=& \sqrt{\frac{\alpha}{\pi}} t_0 \sqrt{\frac{\pi}{\alpha}}\\ &=& t_0 \end{eqnarray*}$

$\langle t^2 \rangle$ の導出

$\langle t^2 \rangle$ は以下で与えられる．
$\begin{eqnarray*} \langle t^2 \rangle &=& \int t^2 | s(t) |^2dt \end{eqnarray*}$
$\langle t \rangle$ を導出した際の結果を用いて，
$\begin{eqnarray*} \langle t^2 \rangle &=& \int t^2 | s(t) |^2dt &=& \sqrt{\frac{\alpha}{\pi}}\int t^2 \mathrm{e}^{-\alpha(t-t_0)^2} dt \end{eqnarray*}$

$\int t^2 \mathrm{e}^{-\alpha(t-t_0)^2} dt$ のところを解く．
$\begin{eqnarray*} \int t^2 \mathrm{e}^{-\alpha(t-t_0)^2} dt &=& \int (t-t_0)^2 \mathrm{e}^{-\alpha(t-t_0)^2}dt + 2t_0 \int t \mathrm{e}^{-\alpha(t-t_0)^2}dt - {t_0}^2 \int \mathrm{e}^{-\alpha(t-t_0)^2}dt\\ &=& \frac{1}{2\alpha} \sqrt{\frac{\pi}{\alpha}} +2t_0 \times t_0 \sqrt{\frac{\pi}{\alpha}} - {t_0} ^2 \times \sqrt{\frac{\pi}{\alpha}}\\ &=&\frac{1}{2\alpha} \sqrt{\frac{\pi}{\alpha}} + {t_0} ^2 \sqrt{\frac{\pi}{\alpha}} \end{eqnarray*}$
（ガウス積分より　 $\int (t-t_0)^2 \mathrm{e}^{-\alpha(t-t_0)^2}dt = \int v^2 \mathrm{e}^{-\alpha v^2}dv = \frac{1}{2\alpha} \sqrt{\frac{\pi}{\alpha}}$ を用いた）

よって，
$\begin{eqnarray*} \langle t^2 \rangle &=& \sqrt{\frac{\alpha}{\pi}}\int t^2 \mathrm{e}^{-\alpha(t-t_0)^2} dt\\ &=& \sqrt{\frac{\alpha}{\pi}} \left( \frac{1}{2\alpha} \sqrt{\frac{\pi}{\alpha}} + {t_0} ^2 \sqrt{\frac{\pi}{\alpha}} \right)\\ &=& \frac{1}{2\alpha} +{t_0} ^2 \end{eqnarray*}$

以上より，
$\begin{eqnarray*} {\sigma_t}^2 &=& \langle t^2 \rangle - \langle t \rangle^2\\ &=&\frac{1}{2\alpha} +{t_0} ^2 - {t_0} ^2\\ &=& \frac{1}{2\alpha} \end{eqnarray*}$

2018-11-01

メモ：コーエンクラス　核関数を使うとクロス項が消えるりくつ

信号処理

メモ．
検証していないので，情報に対して責任は一切持ちません．

コーエンクラスはウィグナー分布に似た形の関数＝曖昧度関数と核関数の畳み込みとなっている．
核関数は何をしてるかっていうと，どうやらクロス項を抑制しているっぽい．
なんでクロス項を抑制できるの？と疑問である．
その辺は現在勉強中であるが，どうやら以下のようなイメージらしい．

f:id:Yuri-Processing-Club:20181101174248p:plain

核関数はチョイウィリアムス．
値は暗赤色=1，暗青色=0で，原点回りの値を抽出するようなフィルタである．

検証については，
実験的には曖昧度関数などを描いて信号が原点を通る直線になるのか確かめる．
理論的には曖昧度関数の勉強
が必要である．

仕事忙しくなってきたので検証はかなり後になりそう．

2018-10-25

【信号処理基礎】実信号の解析信号への変換方法

信号処理

自分用メモ．計算が合ってるかは自信が無い．
何かあればコメントいただけるとありがたいです．

時間周波数解析手法の一種であるウィグナー分布において，正負の周波数成分を持つ信号や二つ以上の成分から成る信号を分析してみると，その中間部分にスペクトルが発生し，これをクロス項という．本来信号が無いはずの部分にスペクトルが出ているのはよろしくない（そのためクロス項を抑制するような研究が多くなされている）．クロス項抑制のためには実信号を負の周波数を含まないような複素信号に変換してからウィグナー分布の計算を行う．負の周波数を含まない複素信号を解析信号という．今回は実信号から解析信号に変換する計算方法を詳しく書く．

解析信号を $z(t)$ ，実信号を $g(t)$ ， $g(t)$ のフーリエ変換を $G(\omega)$ とする．

$\begin{eqnarray*} z(t) &=& \frac{1}{2\pi} \int_{-\infty}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega\\ &=& 2 \frac{1}{2\pi} \int_{0}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega\\ &=& \frac{1}{\pi} \int_{0}^{\infty} \int_{-\infty}^{\infty} g(k) \mathrm{e}^{-j \omega k} dk \mathrm{e}^{j \omega t} d\omega\\ &=& \frac{1}{\pi} \int_{0}^{\infty} \int_{-\infty}^{\infty} g(k) \mathrm{e}^{j \omega (t-k)} dkd\omega\\ &=& \frac{1}{\pi} \int_{-\infty}^{\infty} g(k) \left( \pi \delta(t-k) + \frac{j}{t-k} \right) dk\\ &=& \int_{-\infty}^{\infty} g(k) \delta(t-k) dk + \frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk \\ &=& g(t) + \frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk \\ &=& g(t)+j\mathcal{H}(g(t)) \end{eqnarray*}$

更に詳しい説明．

これは普通の逆フーリエ変換である．
$z(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega$

次に負の周波数を消し去る．ここの計算が本質部分である．
$\frac{1}{2\pi} \int_{-\infty}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega = 2 \frac{1}{2\pi} \int_{0}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega= \frac{1}{\pi} \int_{0}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega$

次に $G(\omega)=\int_{-\infty}^{\infty} g(k) \mathrm{e}^{-j \omega k} dk$ として入れる．
$\frac{1}{\pi} \int_{0}^{\infty} G(\omega) \mathrm{e}^{j \omega t} d\omega = \frac{1}{\pi} \int_{0}^{\infty} \int_{-\infty}^{\infty} g(k) \mathrm{e}^{-j \omega k} dk \mathrm{e}^{j \omega t} d\omega$

$\mathrm{e}^{-j \omega k}$ と $\mathrm{e}^{j \omega t}$ をくっつけて，積分順序を入れ替える．
$\frac{1}{\pi} \int_{0}^{\infty} \int_{-\infty}^{\infty} g(k) \mathrm{e}^{j \omega (t-k)} dkd\omega = \frac{1}{\pi} \int_{-\infty}^{\infty} g(k) \int_{0}^{\infty} \mathrm{e}^{j \omega(t-k)} d\omega dk$

内側の $\int_{0}^{\infty} \mathrm{e}^{j \omega(t-k)} d\omega$ を計算するが，ここで
$\begin{equation} \int_{0}^{\infty} \mathrm{e}^{j \omega x} d\omega= \pi \delta(x) + \frac{j}{x} \end{equation}$
を用いる．（この計算はここでは詳しく計算しない．結果だけ用いる．）
$\int_{0}^{\infty} \mathrm{e}^{j \omega(t-k) } d\omega= \pi \delta(t-k) + \frac{j}{t-k}$

内側の積分結果を元の式に代入して，第一項と第二項を分離する．
$\frac{1}{\pi} \int_{-\infty}^{\infty} g(k) \left( \pi \delta(t-k) + \frac{j}{t-k} \right) dk= \int_{-\infty}^{\infty} g(k) \left(\delta(t-k) \right) dk + \frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk$

第一項の $\int_{-\infty}^{\infty} g(k) \delta(t-k) dk$ は $k$ についての積分だが， $k=t$ の時のみ $\delta=1$ なので，
$\int_{-\infty}^{\infty} g(k) \delta(t-k) dk=g(t)$

第二項の $\frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk$ だが， $\frac{1}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk$ の部分はヒルベルト変換なので，
$\frac{j}{\pi} \int_{-\infty}^{\infty} \frac{g(k)}{t-k} dk = j\mathcal{H}(g(t))$ と書く．

以上をまとめて，
$z(t) =g(t)+j\mathcal{H}(g(t))$

となる．

参考

2018-10-03

matlab 信号の両端を滑らかに0にする場合はコサインテーパーを使う

matlab 信号処理

　実験用に正弦信号を作成することがある．例として1～1.5秒部分に5kHzの正弦波，1.5～3秒部分に10kHzの正弦波が含まれる信号の時間-振幅グラフを図1に，スペクトログラムを図2に示す（スペクトログラムを表示する部分までのmatlabコードを下に示す）．スペクトログラムを見ると信号の開始時点及び終了時点において，周波数の広い範囲に大きい値が出ている（図3）．これは信号が突然0→1に立ち上がる（終了時点では1→0になる）ことから，その時点においてあらゆる周波数が反応するのは当然である．しかしA[Hz]の正弦信号を入力したらA[Hz]のところにだけ値が出て来て欲しいわけで，そういうときは普通ならばスペクトログラムのウィンドウ幅を長くするなど分析側のパラメータを調整する必要がある．今回は理想的な信号が入ってくる場合の分析器の挙動を見たいので，分析側のパラメータを変えずに，実験用の信号を理想的なものに調整して綺麗な結果を出してみる．

f:id:Yuri-Processing-Club:20181003162409p:plain:w400

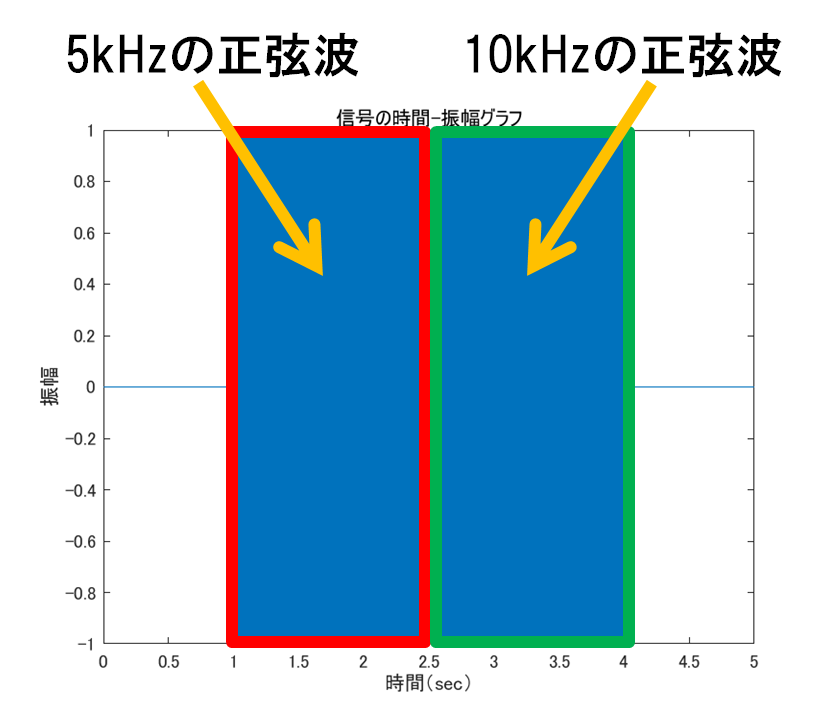
図 1: 信号の時間-振幅グラフ
f:id:Yuri-Processing-Club:20181003161738p:plain:w400

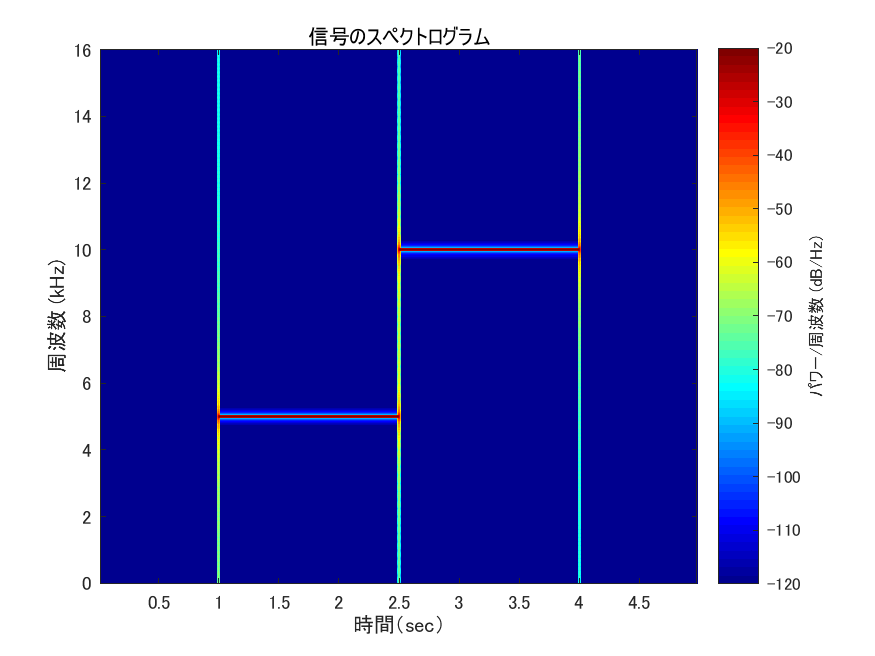
図 2: 信号のスペクトログラム
f:id:Yuri-Processing-Club:20181003163917p:plain:w400

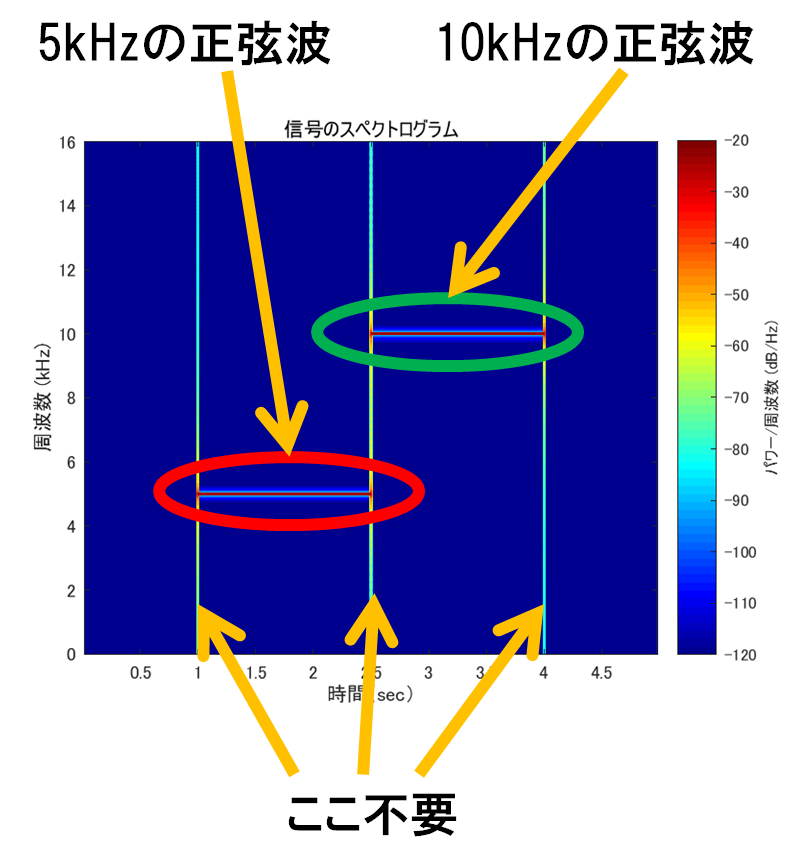
図 3: 信号のスペクトログラム（説明付）

% 
% 信号を生成してスペクトログラムを表示する
% 
clear all;
close all;
clc

Fs = 32000;
SNRdB = -10;

% 信号を生成する
t1 = 1.5;
f1 = 5000;
N = Fs * t1;
t = ((1:N)-1)/Fs;
s1 = sin(2*pi*f1*t);
t2 = 1.5;
f2 = 10000;
N = Fs * t2;
t = ((1:N)-1)/Fs;
s2 = sin(2*pi*f2*t);
s0 = horzcat(s1, s2);
% 信号の前後にpad_time秒間の無音部分をくっつける
pad_time = 1;
s = padarray(s0, [0 round(pad_time * Fs)], 0, 'both');

% 時間グラフを描く
N = length(s);
t = ((1:N)-1)/Fs;
figure
plot(t, s);
title('信号の時間-振幅グラフ');
xlabel('時間（sec）');
ylabel('振幅');

% 信号のスペクトログラムを描画
Nw = 1024;
Nol = Nw*3/4;
NFFT = Nw;
figure;
spectrogram(s, Nw, Nol, NFFT, Fs, 'yaxis'); %ハミング窓
title('信号のスペクトログラム');
xlabel('時間（sec）');
colormap 'jet'
caxis_max = -20;
caxis_min = -120;
caxis([caxis_min, caxis_max]);

つまりこういうことをしたいわけである．

f:id:Yuri-Processing-Club:20181003165529p:plain:w500

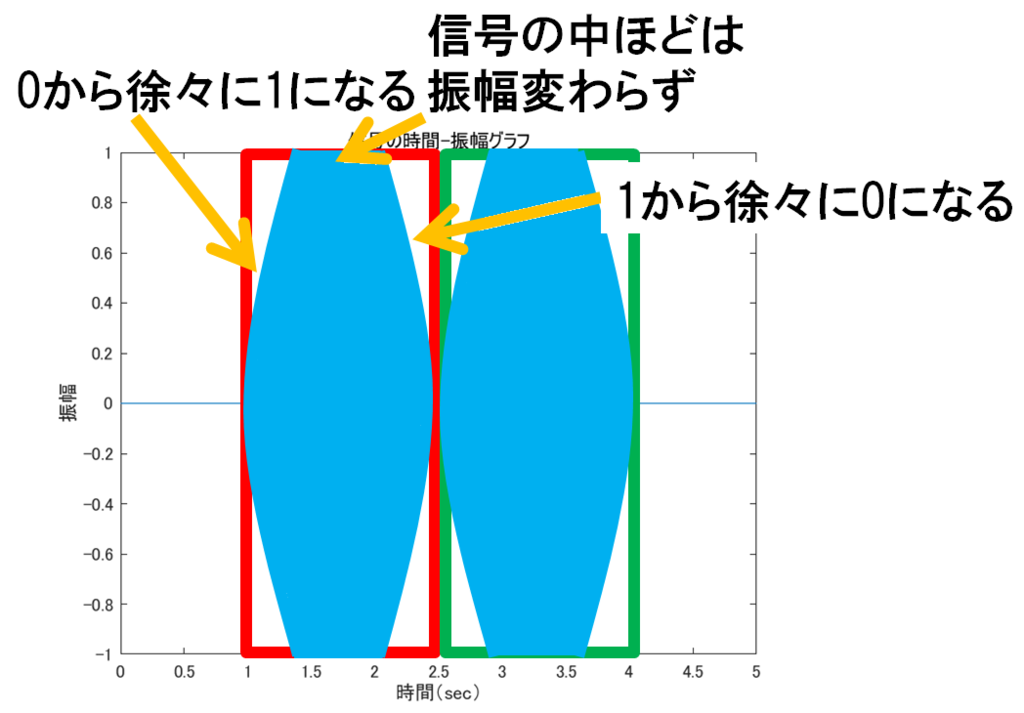
図 4: 立ち上がり立ち下りが滑らかな信号の時間-振幅グラフ

信号の最初と終わりの部分だけ窓関数を掛けたような形である．ネタバレするとコサインテーパーウィンドウを掛けてやればいいわけだが，最初はハンウィンドウを前半後半に分けて信号の最初と終わりにそれぞれ掛けるというやり方を取っていた．

f:id:Yuri-Processing-Club:20181003171032p:plain:w400

図 5: ハンウィンドウ
f:id:Yuri-Processing-Club:20181003171715p:plain

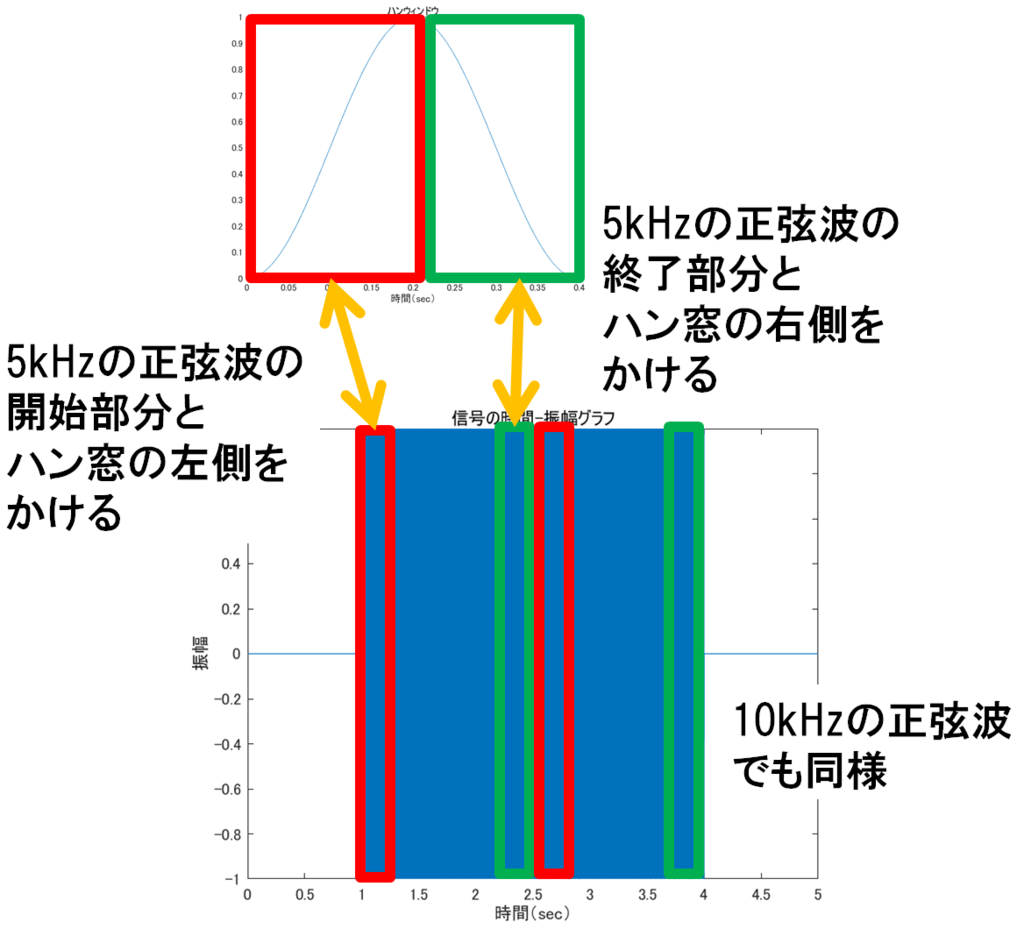
図 6: ハンウィンドウを分割して信号の前後とかけあわせるやつの説明

%
% 上のコードの「信号を生成する」 の部分を下に入れ替える
%
% 信号の両端に少しだけ窓関数をかける
single_sided_window_length_sec = 0.2;% 片側窓関数がかけられる時間
single_sided_window_length = single_sided_window_length_sec * Fs;% 窓関数の片側の長さ
w = hann(single_sided_window_length * 2);% ハン窓を作成
figure
N = length(w);
t = ((1:N)-1)/Fs;
plot(t, w);
title('ハンウィンドウ');
xlabel('時間（sec）');

% 信号を生成する
t1 = 1.5;
f1 = 5000;
N = Fs * t1;
t = ((1:N)-1)/Fs;
s1 = sin(2*pi*f1*t);
% 窓関数をかける
s1(1:single_sided_window_length) = w(1:single_sided_window_length)' .* s1(1:single_sided_window_length);% 左側
s1(end-single_sided_window_length+1:end) = w(single_sided_window_length+1:end)' .* s1(end-single_sided_window_length+1:end);% 右側

t2 = 1.5;
f2 = 10000;
N = Fs * t2;
t = ((1:N)-1)/Fs;
s2 = sin(2*pi*f2*t);
% 窓関数をかける
s2(1:single_sided_window_length) = w(1:single_sided_window_length)' .* s2(1:single_sided_window_length);% 左側
s2(end-single_sided_window_length+1:end) = w(single_sided_window_length+1:end)' .* s2(end-single_sided_window_length+1:end);% 右側

s0 = horzcat(s1, s2);

% 信号の前後にpad_time秒間の無音部分をくっつける
pad_time = 1;
s = padarray(s0, [0 round(pad_time * Fs)], 0, 'both');

ハンウィンドウを分割して信号の前後にかけたものの時間-振幅グラフを図7，スペクトログラムを図8にそれぞれ示す．0→1に滑らかに変化しているので，スペクトログラムで欲しいところだけに信号が表示されている．

f:id:Yuri-Processing-Club:20181003174159p:plain:w400

図 7: 立ち上がり立ち下りを滑らかにした信号の時間-振幅グラフ
f:id:Yuri-Processing-Club:20181003174145p:plain:w400

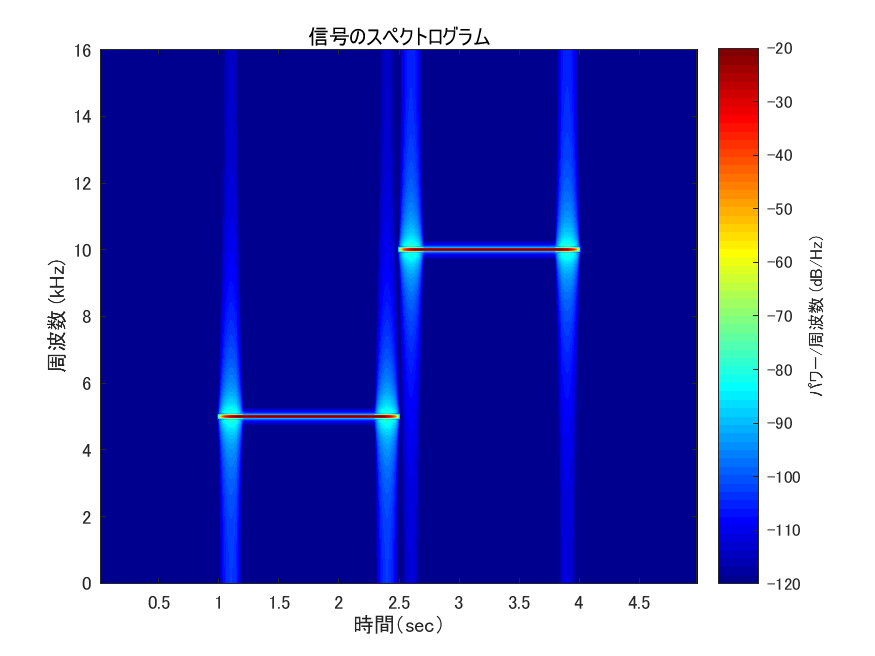
図 8: 立ち上がり立ち下りを滑らかにした信号のスペクトログラム

こんなめんどくさいこと，やる？と思い上司に上手いやり方は無いか相談したところ，そういう場合は普通はコサインテーパーを使うとのこと．jp.mathworks.com
コサインテーパーウィンドウは開始部分及び終了部分がコサインの形をしていて，真ん中あたりは値が1のウィンドウである．信号と同じ長さのコサインテーパーウィンドウを用意して，信号にかけてやればOKである．
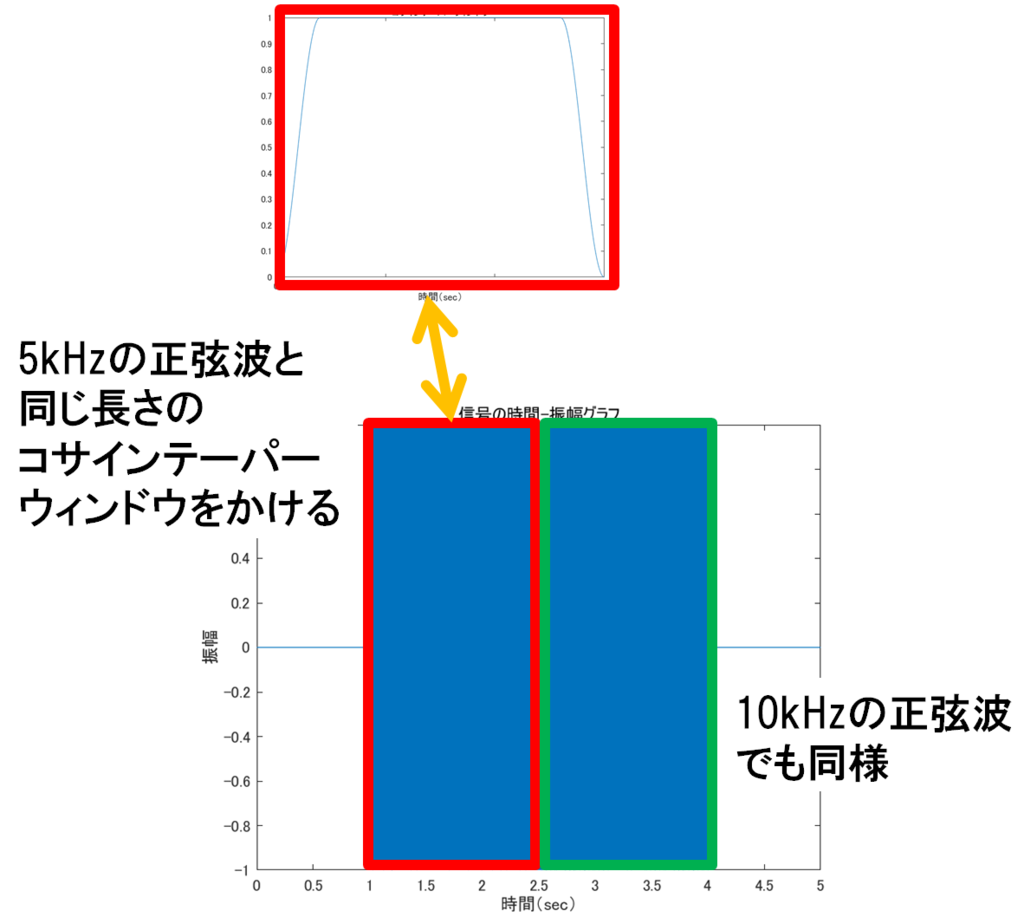
f:id:Yuri-Processing-Club:20181003180521p:plain:w400

f:id:Yuri-Processing-Club:20181003180521p:plain:w400

図 9: 立ち上がり立ち下りを滑らかにした信号の時間-振幅グラフ（コサインテーパー使用）

%
% 上のコードの「信号を生成する」 の部分を下に入れ替える
%
single_sided_window_length_sec = 0.2;% 片側窓関数がかけられる時間

% 信号を生成する
t1 = 1.5;
f1 = 5000;
N = Fs * t1;
t = ((1:N)-1)/Fs;
s1 = sin(2*pi*f1*t);
% 窓関数をかける
window_signal_length_ratio = (single_sided_window_length_sec*2)/t1;% 窓関数がかけられる時間の比
w = tukeywin(N, window_signal_length_ratio);
figure
plot(t, w);
title('コサインテーパーウィンドウ');
xlabel('時間（sec）');
s1 = w' .* s1;

t2 = 1.5;
f2 = 10000;
N = Fs * t2;
t = ((1:N)-1)/Fs;
s2 = sin(2*pi*f2*t);
% 窓関数をかける
window_signal_length_ratio = (single_sided_window_length_sec*2)/t2;% 窓関数がかけられる時間の比
w = tukeywin(N, window_signal_length_ratio);
% 5kHzのコサインテーパーウィンドウと同じなのでグラフは省略
s2 = w' .* s2;

s0 = horzcat(s1, s2);

% 信号の前後にpad_time秒間の無音部分をくっつける
pad_time = 1;
s = padarray(s0, [0 round(pad_time * Fs)], 0, 'both');

f:id:Yuri-Processing-Club:20181003180010p:plain:w400

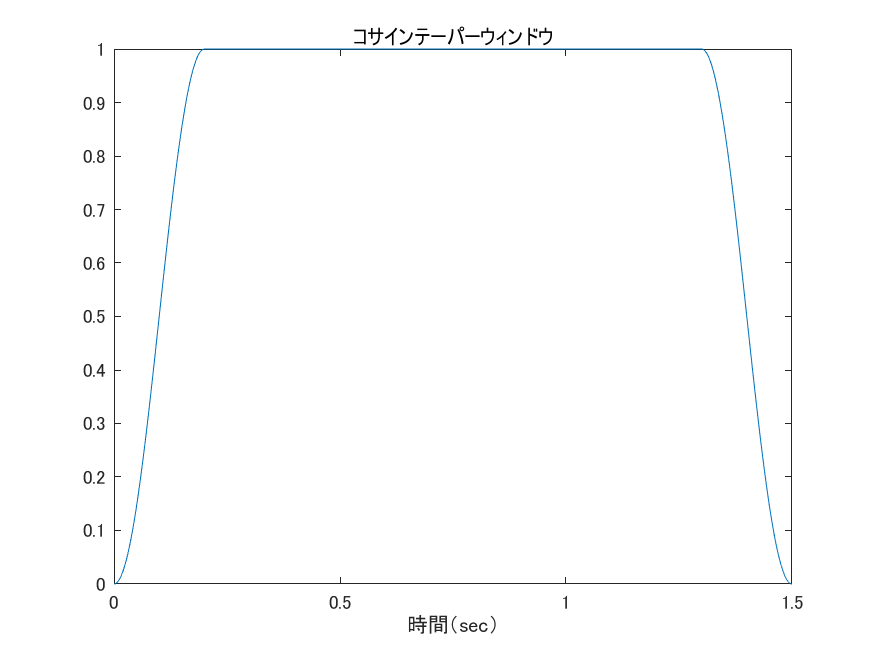
図 10: コサインテーパーウィンドウ
f:id:Yuri-Processing-Club:20181003175920p:plain:w400

図 11: 立ち上がり立ち下りを滑らかにした信号の時間-振幅グラフ（コサインテーパー使用）
f:id:Yuri-Processing-Club:20181003180853p:plain:w400

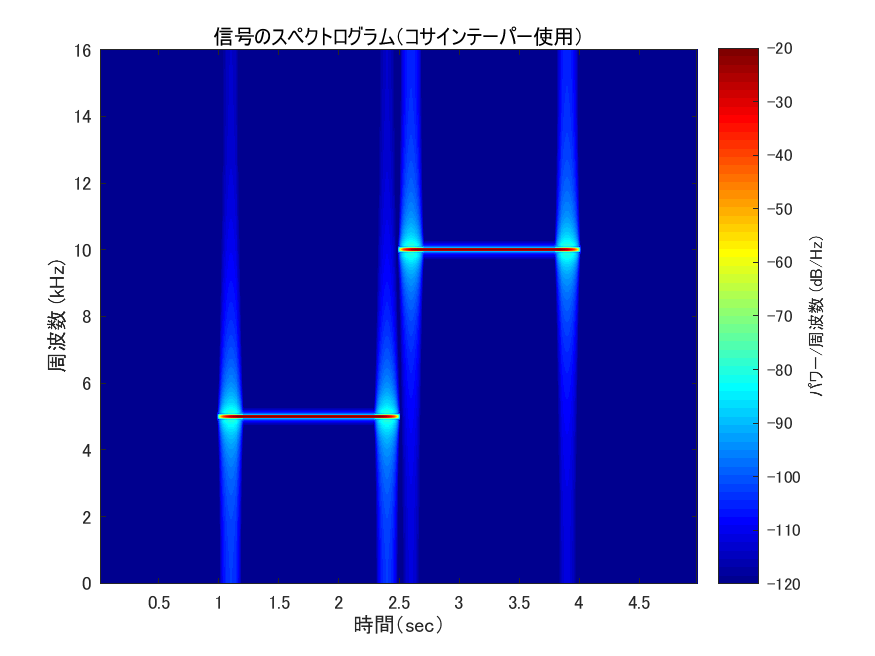
図 12: 立ち上がり立ち下りを滑らかにした信号のスペクトログラム（コサインテーパー使用）

2018-09-27

明かりを消して寝よう：スタンフォード式最高の睡眠

読書

スタンフォード式最高の睡眠

より良い睡眠を取るための本。このような本は書店で目立つ位置に置かれており、過労民族の日本人もどうやら睡眠や休息について意識し始めたっぽい。

私の睡眠スタイルはカスである。
・敷き布団が無い。タイルカーペットの上に寝ている。
・部屋の照明をつけたまま寝ている。（視覚への刺激がある）
・アニメや音楽を流したまま寝ている。（聴覚への刺激がある）
・寝る時間が不規則である。
というか寝落ちするギリギリまでアニメを見ていたりツイッターをやったりしていて、眠気が限界まで来たらその場でそのまま寝るというスタイルである。起きている状態と寝ている状態がかなり曖昧なのである。

大学時代からこういう感じだったので別にいいやと思っていたが、
最近
・日中常に眠い
・足の痛みが取れない
・メンタルをやらかした（病院に行った）
等の不調に悩まされるようになった。

これではまずいと思い、睡眠について真面目に考えるようになり、本を読んでみたわけである。

本で紹介されているTipsの中で簡単に実践できそうなものを探したところ、どうやら明かりを消して寝るというのが良いらしい。寝ている人にライトを照らすと無意識に布団を頭まで被るなど光を遠ざける行動を取る。睡眠時に体は明かりを拒んでいるというわけである。

さっそくアニメを垂れ流すのをやめて部屋を暗くして寝てみたところ、びっくりするほど目覚めが良くなった。日中ほぼ眠気が訪れず、昼寝も必要無くなった。（えっ、こんな簡単に日中のパフォーマンス向上するの？）と驚く限りである。と同時に（なんでこんな簡単なことを今まで実践していなかったの？）と後悔した。

睡眠はどうやら大事っぽい。私レベルに睡眠を軽く考えていた人（布団すら無い人）はそうそういらっしゃらないと思うが、日ごろ眠い、ダルい、疲れが取れないと感じている人は睡眠の質を高めると解決するかもしれない。

以上

それにしても「明かりを消して部屋を暗くして寝るとよく眠れますよ」って異世界世界の主人公のセリフみたいだし、「マジか、知らんかったブログ書くわ」っていう私の反応も異世界の住人のそれだと思う。（もちろん本ではこのような基礎的なTipsだけでなく、もっと目からうろこな話も載っている）

マンガでぐっすり! スタンフォード式最高の睡眠

2018-08-27

メモ：SBI証券　口座開設　マイナンバーは住民票で代用可

メモ．

投資ではSBI証券を利用しており，引越に伴ってSBI証券上で住所変更手続きを行った．
住所変更をする場合は
・マイナンバー確認書類
・個人情報確認書類
を再提出する必要がある．

口座開設の際はマイナンバー確認書類として通知カードを使用した．
しかし，通知カードが見当たらない．
マイナンバー入り住民票で代用できるとは思うが，
WEB上のマイナンバー確認書類の選択画面では
マイナンバーカードか通知カードの２通りしか選べない（マイナンバー入り住民票を選べない）

SBI証券に電話で確認したところ，
マイナンバー確認書類で通知カードを選択し，通知カードをアップロードする場所にマイナンバー入り住民票の画像をアップロードし，
個人情報確認書類にも同じ画像（マイナンバー入り住民票）をアップロードすればOKとのことだった．

おそらくどの証券口座でも同様だろう．（多分）

要はマイナンバーが確認出来れば何でも良いのである．

さっそくマイナンバー入り住民票をアップロードした．
手続きが成功したかについては結果が分かり次第追記する．

yProcessingClub

すみません、許してください

TIME-FREQUENCY ANALYSIS Example 1.3

Example 1.3

解答

解答方針

$\langle \omega \rangle$ の導出

$\langle \omega^2 \rangle$ の導出

まとめ

TIME-FREQUENCY ANALYSIS Example 1.1

Example 1.1

解答

$\langle t \rangle$ の導出

$\langle t^2 \rangle$ の導出

メモ：コーエンクラス　核関数を使うとクロス項が消えるりくつ

【信号処理基礎】実信号の解析信号への変換方法

matlab 信号の両端を滑らかに0にする場合はコサインテーパーを使う

明かりを消して寝よう：スタンフォード式最高の睡眠

メモ：SBI証券　口座開設　マイナンバーは住民票で代用可