yProcessingClub

すみません、許してください

振幅一定，周波数一定の2信号の曖昧度関数を求めよ

信号処理

曖昧度関数とは？

曖昧度関数（Ambiguity function，不確定性関数）はウィグナービレ分布に似た形の式である．
A_z(\nu, \tau) =\int z\left(t+\frac{\tau}{2}\right)z^*\left(t-\frac{\tau}{2}\right) \mathrm{e}^{j 2 \pi \nu t}dt\\
と定義される．

また，Signal Kernel K_z(t, \tau) = z \left( t + \frac{\tau}{2} \right) z^* \left( t - \frac{\tau}{2} \right)を用いて，
A_z(\nu, \tau)=\int K_z(t, \tau) \mathrm{e}^{j 2 \pi \nu t}dt\\
とも書ける．


ウィグナービレ分布
W_z(t, f)=\int K_z(t, \tau) \mathrm{e}^{-j 2 \pi f \tau}d\tau\\
と比較すると，
Signal Kernel K_z(t, \tau) = z \left( t + \frac{\tau}{2} \right) z^* \left( t - \frac{\tau}{2} \right)を
t \to \nuで逆フーリエ変換するのが曖昧度関数
\tau \to fでフーリエ変換するのがウィグナービレ分布
である．

\tau，\nuはそれぞれ時間的，周波数的なナニカであり，
これらをlag(or time shift)，doppler(or frequency shift)と言う．

問題

z(t)= A_1 \mathrm{e}^{j 2 \pi f_1 t} + A_2 \mathrm{e}^{j 2 \pi f_2 t}の曖昧度関数を求めよ．


解法

yuri-processing-club.hatenablog.com

この記事より，
z(t)= A_1 \mathrm{e}^{j 2 \pi f_1 t} + A_2 \mathrm{e}^{j 2 \pi f_2 t}のSignal Kernelは，
K_z(t,\tau) = A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau}


\begin{eqnarray*} &&A_z(\nu, \tau)\\ &=&\int K_z(t, \tau) \mathrm{e}^{j 2 \pi \nu t}dt\\ &=& \int \left( A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \right) \mathrm{e}^{j 2 \pi \nu t}dt\\ &=& A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} \int \mathrm{e}^{j 2 \pi \nu t}dt + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} \int \mathrm{e}^{j 2 \pi \nu t}dt\\ &&+ 2 A_1 A_2 \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \int \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \nu t}dt\\ &=& A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} \delta (\nu) + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} \delta (\nu)+ 2 A_1 A_2 \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \delta \left(\nu + \left( f_2 - f_1 \right) \right)\\ \end{eqnarray*}
となり計算終了である．


解答

z(t)= A_1 \mathrm{e}^{j 2 \pi f_1 t} + A_2 \mathrm{e}^{j 2 \pi f_2 t}の曖昧度関数は

A_z(\nu, \tau) = A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} \delta (\nu) + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} \delta (\nu)+ 2 A_1 A_2 \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \delta \left(\nu + \left( f_2 - f_1 \right) \right)


曖昧度関数のグラフ

曖昧度関数のグラフを描く．複素数となっていてこのままではグラフを描くのは無理なので，絶対値を取って，
A_1^2 \delta (\nu) + A_2^2 \delta (\nu)+ 2 A_1 A_2 \delta \left(\nu + \left( f_2 - f_1 \right) \right)
のグラフを描いてみると，下のようになる．
f:id:Yuri-Processing-Club:20181116182204p:plain

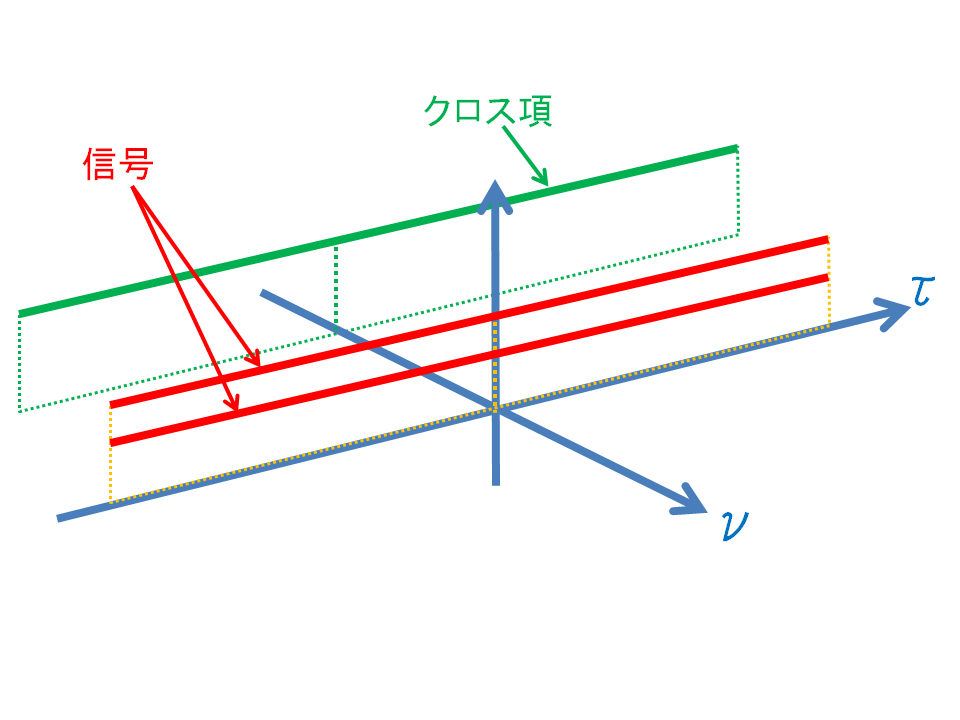
曖昧度関数では，信号は原点を通り，クロス項は原点を通らないことが分かる．

振幅一定，周波数一定の2信号のウィグナービレ分布を求めよ

信号処理

ウィグナービレ分布とは？

ウィグナービレ分布は時間周波数解析手法の一つであり，
W_z(t, f)=\int z\left(t+\frac{\tau}{2}\right)z^*\left(t-\frac{\tau}{2}\right) \mathrm{e}^{-j 2 \pi f \tau}d\tau\\
と定義される．

また，Signal Kernel K_z(t, \tau) = z \left( t + \frac{\tau}{2} \right) z^* \left( t - \frac{\tau}{2} \right)と定義すると，
W_z(t, f)=\int K_z(t, \tau) \mathrm{e}^{-j 2 \pi f \tau}d\tau\\
とも書ける．

問題

z(t)= A_1 \mathrm{e}^{j 2 \pi f_1 t} + A_2 \mathrm{e}^{j 2 \pi f_2 t}のウィグナービレ分布を求めよ．


解法

yuri-processing-club.hatenablog.com

この記事より，
z(t)= A_1 \mathrm{e}^{j 2 \pi f_1 t} + A_2 \mathrm{e}^{j 2 \pi f_2 t}のSignal Kernelは，
K_z(t,\tau) = A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau}


\begin{eqnarray*} &&W_z(t, f)\\ &=&\int K_z(t, \tau) \mathrm{e}^{-j 2 \pi f \tau}d\tau\\ &=& \int \left( A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \right) \mathrm{e}^{-j 2 \pi f \tau}d\tau\\ &=& \int A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} \mathrm{e}^{-j 2 \pi f \tau}d\tau + \int A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} \mathrm{e}^{-j 2 \pi f \tau}d\tau\\ &&+ \int 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \mathrm{e}^{-j 2 \pi f \tau}d\tau\\ &=& A_1^2 \int \mathrm{e}^{j 2 \pi f_1 \tau} \mathrm{e}^{-j 2 \pi f \tau}d\tau + A_2^2 \int \mathrm{e}^{j 2 \pi f_2 \tau} \mathrm{e}^{-j 2 \pi f \tau}d\tau\\ &&+ 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \int \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \mathrm{e}^{-j 2 \pi f \tau}d\tau\\ &=& A_1^2 \delta (f-f_1) + A_2^2 \delta (f-f_2) + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \delta \left( f - \frac{f_1+f_2}{2}\right) \end{eqnarray*}
となり計算終了である．


解答

z(t)= A_1 \mathrm{e}^{j 2 \pi f_1 t} + A_2 \mathrm{e}^{j 2 \pi f_2 t}のウィグナービレ分布は

W_z(t,f) = A_1^2 \delta (f-f_1) + A_2^2 \delta (f-f_2) + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \delta \left( f - \frac{f_1+f_2}{2}\right)


クロス項

A_1^2 \delta(f-f_1)及び A_2^2 \delta(f-f_2)は期待通りの項である．2 A_1 A_2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \delta \left( f - \frac{f_1+f_2}{2} \right)は本来存在しないスペクトルであり，これをクロス項と言う．クロス項は2信号の中間の位置に出ると言われているが，計算結果を見ると，確かにf_1及びf_2の中間の周波数\frac{f_1+f_2}{2}の部分に発生していることが分かる．また，\cos \left( 2 \pi \left( f_2 - f_1 \right) t \right)を見ると分かるが，クロス項は時間方向に周波数f_2-f_1で振動している．
f:id:Yuri-Processing-Club:20181115161108p:plain
図にするとこんな感じだろう．

振幅一定，周波数一定の2信号のSignal Kernelを求めよ

信号処理

Signal Kernelとは？

K_z(t, \tau) = z \left( t + \frac{\tau}{2} \right) z^* \left( t - \frac{\tau}{2} \right)
と定義され，ウィグナービレ分布などに用いられる．

問題

z(t)= A_1 \mathrm{e}^{j 2 \pi f_1 t} + A_2 \mathrm{e}^{j 2 \pi f_2 t}のSignal Kernelを求めよ．


解法

z^*(t)= A_1 \mathrm{e}^{-j 2 \pi f_1 t} + A_2 \mathrm{e}^{-j 2 \pi f_2 t}


Signal Kernelは
\begin{eqnarray*} K_z(t, \tau) &=& z \left( t + \frac{\tau}{2} \right) z^* \left( t - \frac{\tau}{2} \right)\\ &=& \left( A_1 \mathrm{e}^{j 2 \pi f_1 \left( t + \frac{\tau}{2} \right)} + A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} \right) \left( A_1 \mathrm{e}^{-j 2 \pi f_1 \left( t - \frac{\tau}{2} \right)} + A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)} \right) \\ &=&A_1 \mathrm{e}^{j 2 \pi f_1 \left( t + \frac{\tau}{2} \right)} A_1 \mathrm{e}^{-j 2 \pi f_1 \left( t - \frac{\tau}{2} \right)} + A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)}\\ && + A_1 \mathrm{e}^{j 2 \pi f_1 \left( t + \frac{\tau}{2} \right)} A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)} + A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} A_1 \mathrm{e}^{-j 2 \pi f_1 \left( t - \frac{\tau}{2} \right)}\\ &=& A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \end{eqnarray*}
となり，計算終了である．
さらに詳しい途中式は下で書くので，気になる方はスクロールされたし．



解答

z(t)= A_1 \mathrm{e}^{j 2 \pi f_1 t} + A_2 \mathrm{e}^{j 2 \pi f_2 t}のSignal Kernel K_z(t,\tau)は
K_z(t,\tau) = A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau}



詳しい途中式

\begin{eqnarray*} K_z(t, \tau) &=&A_1 \mathrm{e}^{j 2 \pi f_1 \left( t + \frac{\tau}{2} \right)} A_1 \mathrm{e}^{-j 2 \pi f_1 \left( t - \frac{\tau}{2} \right)} + A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)}\\ && + A_1 \mathrm{e}^{j 2 \pi f_1 \left( t + \frac{\tau}{2} \right)} A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)} + A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} A_1 \mathrm{e}^{-j 2 \pi f_1 \left( t - \frac{\tau}{2} \right)}\\ &=& A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \end{eqnarray*}
ここの部分は計算を省略したので，詳しく書く．
項ごとに計算する．

第1項

\begin{eqnarray*} A_1 \mathrm{e}^{j 2 \pi f_1 \left( t + \frac{\tau}{2} \right)} A_1 \mathrm{e}^{-j 2 \pi f_1 \left( t - \frac{\tau}{2} \right)} &=& A_1 \mathrm{e}^{j 2 \pi f_1 t} \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} } A_1 \mathrm{e}^{-j 2 \pi f_1 t} \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} }\\ &=& A_1 A_1 \mathrm{e}^{j 2 \pi f_1 t} \mathrm{e}^{-j 2 \pi f_1 t} \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} } \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} }\\ &=& A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} \end{eqnarray*}

(なお，A_1 A_1 = A_1^2， \mathrm{e}^{j 2 \pi f_1 t} \mathrm{e}^{-j 2 \pi f_1 t}=1， \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} } \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} } = \mathrm{e}^{j 2 \pi f_1 \tau}である）

第2項

A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)}は上の計算でA_1 \to A_2，f_1 \to f_2とすれば後は全く同じ計算である．
\begin{eqnarray*} A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)} &=& A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} \end{eqnarray*}


第3項

\begin{eqnarray*} A_1 \mathrm{e}^{j 2 \pi f_1 \left( t + \frac{\tau}{2} \right)} A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)}&=& A_1 \mathrm{e}^{j 2 \pi f_1 t} \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} } A_2 \mathrm{e}^{-j 2 \pi f_2 t} \mathrm{e}^{j 2 \pi f_2 \frac{\tau}{2} }\\ &=& A_1 A_2 \mathrm{e}^{j 2 \pi f_1 t} \mathrm{e}^{-j 2 \pi f_2 t} \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} } \mathrm{e}^{j 2 \pi f_2 \frac{\tau}{2} }\\ &=& A_1 A_2 \mathrm{e}^{-j 2 \pi \left(f_2 - f_1 \right)t} \mathrm{e}^{j 2 \pi \frac{f_1 + f_2}{2}\tau} \end{eqnarray*}

第4項

\begin{eqnarray*} A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} A_1 \mathrm{e}^{-j 2 \pi f_1 \left( t - \frac{\tau}{2} \right)}&=& A_2 \mathrm{e}^{j 2 \pi f_2 t} \mathrm{e}^{j 2 \pi f_2 \frac{\tau}{2} } A_1 \mathrm{e}^{-j 2 \pi f_1 t} \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} }\\ &=& A_1 A_2 \mathrm{e}^{-j 2 \pi f_1 t} \mathrm{e}^{j 2 \pi f_2 t} \mathrm{e}^{j 2 \pi f_1 \frac{\tau}{2} } \mathrm{e}^{j 2 \pi f_2 \frac{\tau}{2} }\\ &=& A_1 A_2 \mathrm{e}^{j 2 \pi \left(f_2 - f_1 \right)t} \mathrm{e}^{j 2 \pi \frac{f_1 + f_2}{2}\tau} \end{eqnarray*}

第3項+第4項

第3項と第4項を統合する．
A_1 A_2 \mathrm{e}^{-j 2 \pi \left(f_2 - f_1 \right)t} \mathrm{e}^{j 2 \pi \frac{f_1 + f_2}{2}\tau} +A_1 A_2 \mathrm{e}^{j 2 \pi \left(f_2 - f_1 \right)t} \mathrm{e}^{j 2 \pi \frac{f_1 + f_2}{2}\tau} \\ =A_1 A_2 \ \mathrm{e}^{j 2 \pi \frac{f_1 + f_2}{2}\tau} \left( \mathrm{e}^{-j 2 \pi \left(f_2 - f_1 \right)t} + \mathrm{e}^{j 2 \pi \left(f_2 - f_1 \right)t} \right)\\ =A_1 A_2 \ \mathrm{e}^{j 2 \pi \frac{f_1 + f_2}{2}\tau} \left( \mathrm{e}^{j 2 \pi \left(f_2 - f_1 \right)t} + \mathrm{e}^{-j 2 \pi \left(f_2 - f_1 \right)t} \right) \ \ \cdots (*)\\

ここでオイラーの公式 \cos \theta = \frac{\mathrm{e}^{j \theta} + \mathrm{e}^{-j \theta}}{2} \iff \mathrm{e}^{j \theta} + \mathrm{e}^{-j \theta} = 2 \cos \theta より，
\begin{eqnarray*} \mathrm{e}^{j 2 \pi \left(f_2 - f_1 \right)t} + \mathrm{e}^{-j 2 \pi \left(f_2 - f_1 \right)t} &=& 2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \end{eqnarray*}

よって，
\begin{eqnarray*} (*) &=& A_1 A_2 \mathrm{e}^{j 2 \pi \left(f_2 - f_1 \right)t} 2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right)\\ &=& 2 A_1 A_2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left(f_2 - f_1 \right)t} \end{eqnarray*}


第1項+第2項+第3項+第4項

以上の結果から
\begin{eqnarray*} K_z(t, \tau) &=&A_1 \mathrm{e}^{j 2 \pi f_1 \left( t + \frac{\tau}{2} \right)} A_1 \mathrm{e}^{-j 2 \pi f_1 \left( t - \frac{\tau}{2} \right)} + A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)}\\ && + A_1 \mathrm{e}^{j 2 \pi f_1 \left( t + \frac{\tau}{2} \right)} A_2 \mathrm{e}^{-j 2 \pi f_2 \left( t - \frac{\tau}{2} \right)} + A_2 \mathrm{e}^{j 2 \pi f_2 \left( t + \frac{\tau}{2} \right)} A_1 \mathrm{e}^{-j 2 \pi f_1 \left( t - \frac{\tau}{2} \right)}\\ &=& A_1^2 \mathrm{e}^{j 2 \pi f_1 \tau} + A_2^2 \mathrm{e}^{j 2 \pi f_2 \tau} + 2 A_1 A_2 \cos \left( 2\pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2}\right) \tau} \end{eqnarray*}
が導かれる．

2信号のウィグナービレ分布を求めよ

信号処理

ウィグナービレ分布

2信号のウィグナービレ分布は？

yuri-processing-club.hatenablog.com
この記事では
信号が1つ(s(t)=\cos(2 \pi f_c t))のウィグナービレ分布を求め，
W_z(t,f) = \delta(f-f_c)
となった．

それでは2信号ではどうなるだろうか．

問題

s(t)=\cos(2 \pi f_1 t) + \cos(2 \pi f_2 t)のウィグナービレ分布を求めよ．


解法

まずs(t)を解析信号z(t)に変換する．
z(t)=\mathrm{e}^{j 2 \pi f_1 t} + \mathrm{e}^{j 2 \pi f_2 t}

また，
z^*(t)=\mathrm{e}^{-j 2 \pi f_1 t} + \mathrm{e}^{-j 2 \pi f_2 t}

次にSignal Kernelを求める．

z\left(t+\frac{\tau}{2}\right)z^*\left(t-\frac{\tau}{2}\right)\\ =\left( \mathrm{e}^{j 2 \pi f_1 \left( t +\frac{\tau}{2} \right)} + \mathrm{e}^{j 2 \pi f_2 \left( t +\frac{\tau}{2} \right)} \right) \left(\mathrm{e}^{-j 2 \pi f_1 \left( t -\frac{\tau}{2} \right)} + \mathrm{e}^{-j 2 \pi f_2 \left( t -\frac{\tau}{2} \right)}\right)\\ = \mathrm{e}^{j 2 \pi f_1 \tau} + \mathrm{e}^{j 2 \pi f_2 \tau} + 2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2} \right) \tau}


よって，ウィグナービレ分布は，

\begin{eqnarray*} W_z(t,f) &=& \int z\left(t+\frac{\tau}{2}\right)z^*\left(t-\frac{\tau}{2}\right) \mathrm{e}^{-j 2 \pi f \tau} d\tau\\ &=& \int \left( \mathrm{e}^{j 2 \pi f_1 \tau} + \mathrm{e}^{j 2 \pi f_2 \tau} + 2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2} \right) \tau} \right) \mathrm{e}^{-j 2 \pi f \tau} d\tau\\ &=& \int \mathrm{e}^{j 2 \pi f_1 \tau}\mathrm{e}^{-j 2 \pi f \tau}d\tau + \int \mathrm{e}^{j 2 \pi f_2 \tau}\mathrm{e}^{-j 2 \pi f \tau}d\tau\\ && +\int \left( 2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2} \right) \tau} \right) \mathrm{e}^{-j 2 \pi f \tau}d\tau\\ &=& \int \mathrm{e}^{j 2 \pi f_1 \tau}\mathrm{e}^{-j 2 \pi f \tau}d\tau + \int \mathrm{e}^{j 2 \pi f_2 \tau}\mathrm{e}^{-j 2 \pi f \tau}d\tau \\ &&+ 2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \int \mathrm{e}^{j 2 \pi \left( \frac{f_1+f_2}{2} \right) \tau} \mathrm{e}^{-j 2 \pi f \tau}d\tau\\ &=& \delta(f-f_1) + \delta(f-f_2) + 2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \delta \left( f - \frac{f_1+f_2}{2} \right) \end{eqnarray*}
となり計算終了である．


答え

s(t)=\cos(2 \pi f_1 t) + \cos(2 \pi f_2 t)のウィグナービレ分布は，
W_z(t,f) = \delta(f-f_1) + \delta(f-f_2) + 2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \delta \left( f - \frac{f_1+f_2}{2} \right)



クロス項

\delta(f-f_1)及び\delta(f-f_2)は期待通りの項である．2 \cos \left( 2 \pi \left( f_2 - f_1 \right) t \right) \delta \left( f - \frac{f_1+f_2}{2} \right)は本来存在しないスペクトルであり，これをクロス項と言う．クロス項は2信号の中間の位置に出ると言われているが，計算結果を見ると，確かにf_1及びf_2の中間の周波数\frac{f_1+f_2}{2}の部分に発生していることが分かる．また，\cos \left( 2 \pi \left( f_2 - f_1 \right) t \right)を見ると分かるが，クロス項は時間方向に周波数f_2-f_1で振動している．


図解

f:id:Yuri-Processing-Club:20181115161108p:plain
ウィグナービレ分布を図にするとこんな感じだろう（多分）．

AM変調信号のウィグナービレ分布

信号処理

今回も引き続き情報の精度については自信が無い．
メモとしてブログに残しておく．

yuri-processing-club.hatenablog.com

この記事で，z(t)=A(t)\mathrm{e}^{j \phi (t)}のウィグナービレ分布は

W_z(t,f) = \mathcal{W}_A(t, f-f_i(t))
になることを計算で確かめた．

本記事ではこれの意味を考えていく．


f:id:Yuri-Processing-Club:20181114193536p:plain
周波数一定（f_0）の信号をf_cで変調しよう．



f:id:Yuri-Processing-Club:20181114193459p:plain
スペクトルで見ると，このようにf_cだけ平行移動する形となる．

この例では元の信号の周波数f_0も搬送波f_cも時間変化しない．




f:id:Yuri-Processing-Club:20181114193558p:plain
時間周波数平面で書き直してみるとこんな感じ．周波数の時間変化は無いのでグラフの傾きは0である．



次にA(t)の周波数が時間変化する信号を考える．
搬送波周波数は一定なので，
f:id:Yuri-Processing-Club:20181114193824p:plain
同じようにf_cだけ平行移動した形となる．



次にA(t)もf_cも変調する場合を考える．
f:id:Yuri-Processing-Club:20181114194006p:plain
ある時点t_1におけるもとの信号の周波数\pm f(t_1)はその時点での搬送波の周波数f_c(t_1)だけずれるので，変調後の周波数f'=f_c(t_1) \pm f(t_1)



f:id:Yuri-Processing-Club:20181114200201p:plain
時間-周波数平面W(t,f)で考えると，変調後のある点W_z(t_1,f_1)は，変調前はf_c(t_1)だけ下にあった．つまり変調前は\mathcal{W}_A(t_1,f_1-f_c(t_1))の位置にあった．

変調する搬送波周波数f_c(t)を瞬時周波数f_i(t)に書き直して，W_z(t,f) = \mathcal{W}_A(t, f-f_i(t))である．



振幅A(t)を瞬時周波数f_i(t)を使ってAM変調した信号のウィグナービレ分布W_zは，f_i(t)とA(t)のウィグナー分布 \mathcal{W}_Aを使って表せることが分かる．
若干煙に巻いた部分はあるが，何となくの解釈はこんな感じでよいかもしれないし，よくないかもしれない．

メモ：周波数シフト計算

信号処理


72ページより計算メモ．


ぜんぜんわからん・・・
とりあえず計算メモだけ残しておく．

\begin{eqnarray*} k_z(\nu,f)&=&\int W_z(t,f) \mathrm{e}^{-j 2 \pi \nu t} dt\\ &=&\int \left( \int z(t+\tau/2)z^*(t-\tau/2) \mathrm{e}^{-j 2 \pi f \tau} d\tau \right) \mathrm{e}^{-j 2 \pi \nu t} dt\\ &=& \int \int z(t+\tau/2)z^*(t-\tau/2)\mathrm{e}^{-j 2 \pi (f \tau + \nu t)} dt d\tau \end{eqnarray*}


u = t+\frac{\tau}{2}=U(t, \tau)，v=t-\frac{\tau}{2}=V(t,\tau)と置くと，

t=\frac{1}{2}(u+v)=T(u,v)，\tau=u-v=\mathcal{T}(u,v)

\begin{eqnarray*} dtd\tau &=& \mathrm{ABS} \left( \mathrm{det} \left( \begin{array}{cc} \partial T / \partial u & \partial T / \partial v \\ \partial \mathcal{T} / \partial u & \partial \mathcal{T} / \partial v \\ \end{array} \right) \right) dudv\\ &=& \mathrm{ABS} \left( \mathrm{det} \left( \begin{array}{cc} 1/2 & 1/2 \\ 1 & -1 \\ \end{array} \right) \right) dudv\\ &=& \mathrm{ABS} \left( -1/2 - 1/2 \right)dudv\\ &=& \mathrm{ABS} \left( -1 \right)dudv\\ &=& dudv\ \end{eqnarray*}
↑この辺かなり微妙である．ヤコビアン行列が云々らしいが・・・？

よって，

\begin{eqnarray*} k_z(\nu,f)&=& \int \int z(t+\tau/2)z^*(t-\tau/2)\mathrm{e}^{-j 2 \pi (f \tau + \nu t)} dt d\tau \\ &=& \int \int z(u)z^*(v)\mathrm{e}^{-j 2 \pi (f (u-v)+ \nu \frac{1}{2}(u+v))} dudv \\ &=& \int \int z(u)z^*(v)\mathrm{e}^{-j 2 \pi (fu-fv+ \frac{1}{2}\nu u + \frac{1}{2} \nu v)} dudv \\ &=& \int \int z(u)z^*(v)\mathrm{e}^{-j 2 \pi (f + \frac{1}{2}\nu)u } \mathrm{e}^{j 2 \pi (f - \frac{1}{2}\nu)v } dudv \\ &=& \int z(u)\mathrm{e}^{-j 2 \pi (f + \frac{1}{2}\nu)u } du \int z^*(v)\mathrm{e}^{j 2 \pi (f - \frac{1}{2}\nu)v } dv \\ &=& Z \left( f+\frac{\nu}{2} \right) Z^* \left( f-\frac{\nu}{2} \right) \end{eqnarray*}

よって，
W_z(t,f)=\int Z \left( f+\frac{\nu}{2} \right) Z^* \left( f-\frac{\nu}{2} \right) \mathrm{e}^{j 2 \pi \nu t} d\nu


\nuを周波数シフト（またはドップラー）と言うそうだが，何がどうなってるのかぜんぜんわからん

ウィグナー分布の求め方は2通りあって，
1.時間ドメインで相関関数的なやつ（instantaneous autocorrelation function, IAF）K_z(t,f)を求めてフーリエ変換
2.周波数ドメインで相関関数的なやつ（spectral correlation function, SCF）k_z(\nu,f)を求めて逆フーリエ変換（本記事の話）
みたいな感じかな・・・・・・？

ふわふわしたことを言うが，おそらく時間-周波数平面として(t - f)平面と(\tau - \nu)平面があるっぽくて，後者は曖昧度関数が持つ平面っぽい．

LFM信号のウィグナービレ分布

信号処理


71ページから解説．

yuri-processing-club.hatenablog.com
ここと併せて読まれたし．


上の記事では信号としてz(t)=\mathrm{e}^{j \phi (t)}を考えた．

今回は振幅が時間変化する信号z(t)=A(t)\mathrm{e}^{j \phi (t)}を考える．

Signal Kernelは
\begin{eqnarray*} K_z(t,\tau) &=& z(t+\tau/2)z^*(t-\tau/2)\\ &=& A(t+\tau/2)\mathrm{e}^{j \phi (t+\tau/2)} A(t-\tau/2)\mathrm{e}^{-j \phi (t-\tau/2)}\\ &=& A(t+\tau/2) A(t-\tau/2) \mathrm{e}^{j \phi (t+\tau/2)}\mathrm{e}^{-j \phi (t-\tau/2)}\\ &=& A(t+\tau/2) A(t-\tau/2) \mathrm{e}^{j (\phi (t+\tau/2) - \phi (t-\tau/2))}\\ &=& K_A(t,\tau)\mathrm{e}^{j\psi(t,\tau)} \end{eqnarray*}

ここで\phi(t)が二次式ならば，limの近似が行え，
\psi (t, \tau) = \phi ' (t) \tau = 2 \pi f_i (t) \tauである．

よって，
K_z(t,\tau) =K_A(t,\tau)\mathrm{e}^{j2 \pi f_i (t) \tau}

これをフーリエ変換したものがウィグナービレ分布であるから，
\begin{eqnarray*} W_z(t,f) &=& \int K_z(t,\tau) \mathrm{e}^{-j 2 \pi f \tau} d\tau\\ &=& \int K_A(t,\tau)\mathrm{e}^{j2 \pi f_i (t) \tau} \mathrm{e}^{-j 2 \pi f \tau} d\tau\\ &=& \int K_A(t,\tau)\mathrm{e}^{-j2 \pi (f - f_i (t)) \tau} d\tau\\ &=& \mathcal{W}_A(t, f-f_i(t)) \end{eqnarray*}

（区別のため，ウィグナービレ分布をW，ウィグナー分布を\mathcal{W}と書く）